Koutecky-Levich Analysis (RDE)

When the rate of a half reaction occurring at an electrode surface is limited by a combination of mass transport and sluggish kinetics, it is often possible to use a rotating disk electrode to elucidate both the mass transport parameters (such as the diffusion coefficient) and the kinetic parameters (such as the standard rate constant, k⁰) from a properly designed Levich study.  A full treatment of this kind of analysis  Treimer, S.; Tang, A.; Johnson, D. C.  A Consideration of the Application of Koutecký-Levich Plots in the Diagnoses of Charge-Transfer Mechanisms at Rotated Disk Electrodes.  Electroanalysis, 2002, 14(3), 165-171.  is beyond the scope of this document, but the following is a general description of how to extract kinetic information from a set of rotating disk voltammograms.

 

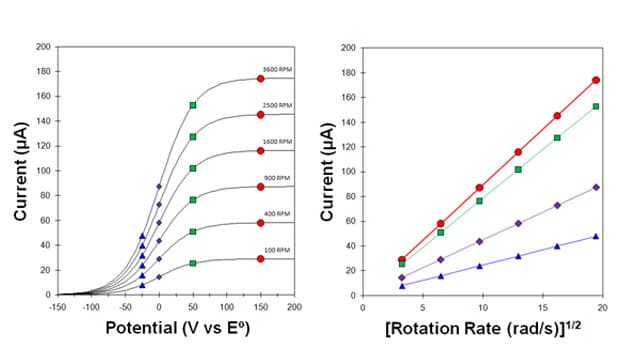
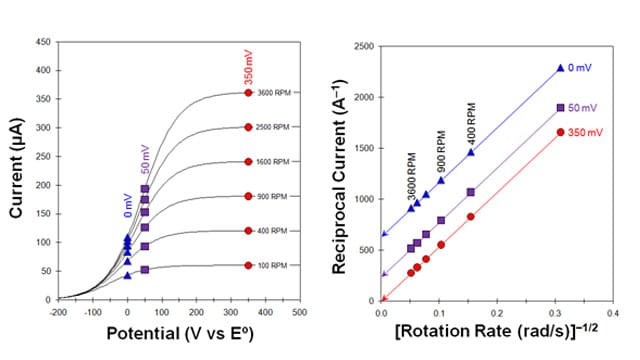
When the electron transfer process at an electrode surface exhibits sluggish kinetics, the voltammogram appears stretched out along the potential axis, and the shape of the sigmoidal wave is slightly distorted.  Comparing a set of voltammograms with facile kinetics (see Figure 1) with a set of voltammograms with sluggish kinetics (see Figure 2), the mass transport limited current plateau (marked by red circles in each figure) is shifted further away from the standard electrode potential (E⁰) when there are slow kinetics.   Stated another way, when a sluggish redox half reaction is studied with a rotating disk electrode, a larger overpotential must be applied to the electrode to overcome the sluggish kinetics and reach the mass transport limited current.

 

 

 

This distortion of the ideal sigmoidal shape of the voltammogram can be exploited as a way to measure the standard rate constant (k⁰).  The general approach is to acquire a set of voltammograms at different rotation rates (i.e., perform a Levich study) and then plot the reciprocal current (sampled at particular locations along the rising portion of each voltammogram) on a Koutecky-Levich Plot.  In the example provided (see Figure 9, Left), the current was sampled at two locations along the rising portion of the voltammograms (at 0 and 50 mV vs E⁰, marked with blue triangles and purple squares) and at one location on the limiting current plateau (at 350 mV vs E⁰, marked with red circles).  A linear relationship is evident (see Figure 2, Right) when these sampled currents are plotted on a Koutecky-Levich Plot.

 

For the set of currents sampled on the limiting current plateau (see Figure 2, Red circles), an extrapolation back to the vertical axis (i.e., to infinite rotation rate) yields a zero intercept.  This is the identical result obtained for a facile half-reaction (see Figure 1, Right) because these currents are sampled at a high enough overpotential that there are no kinetic limitations.  Only mass transport limits the current, and the usual Levich behavior applies.

 

However, for the two sets of currents sampled on the rising portion of the voltammogram (see Figure 2, Blue triangles and purple squares), the extrapolation back to the vertical axis yields non-zero intercepts.  This non-zero intercept indicates a kinetic limitation, meaning that even if mass transport were infinite (i.e., infinite rotation rate), the rate of the half-reaction would still be limited by the slow kinetics at the electrode surface.

 

The linear portion of the data on a Koutecky-Levich plot is described by the Koutecky-Levich equation.

 

Plotting the reciprocal current (1/i) against the reciprocal root of the angular rotation rate (ω^-1/2) yields a straight line with an intercept equal to the reciprocal kinetic current (1/i_K).  The kinetic current is the current that would be observed in the absence of any mass transport limitations.  By measuring the kinetic current at a variety of different overpotentials along the voltammogram, it is possible to determine the standard rate constant for the electrochemical half reaction.  Further details regarding Koutecky-Levich theory, including various forms of the Koutecky-Levich equation which pertain to different electrochemical processes, can be found in the literature.  Treimer, S.; Tang, A.; Johnson, D. C.  A Consideration of the Application of Koutecký-Levich Plots in the Diagnoses of Charge-Transfer Mechanisms at Rotated Disk Electrodes.  Electroanalysis, 2002, 14(3), 165-171.

• Treimer, S.; Tang, A.; Johnson, D. C.  A Consideration of the Application of Koutecký-Levich Plots in the Diagnoses of Charge-Transfer Mechanisms at Rotated Disk Electrodes.  Electroanalysis, 2002, 14(3), 165-171.