
This article is part of the AfterMath Data Organizer Electrochemistry Guide[/call_to_action]
Like most of the other electrochemical techniques offered by the AfterMath software, this experiment begins with an induction period. During the induction period, a set of initial conditions is applied to the electrochemical cell and the cell is allowed to equilibrate to these conditions. The default initial condition involves holding the working electrode potential at the Initial Potential for a brief period of time (i.e., 3 seconds). If the potentiostat is being used to control the rotator speed, the rotator is also spun at the desired Speed during this time. The WaveNow and WaveNano are capable of outputting a potential proportional to the desired rotator speed. This output can then be coupled to the input on an MSR rotator for fully automated control of the rotation speed.
For a typical one segment RDE experiment, after the induction period, the potential of the working electrode is swept linearly at the specified Sweep Rate from the Initial Potential to the Final Potential. Typical sweep rates are . The Typical Results section below shows the effect of sweep rates that are too large.
After the sweep has finished, the experiment concludes with a relaxation period. The default condition during the relaxation period involves holding the working electrode potential at the final potential for an additional brief period of time (i.e., 1 seconds).
At the end of the relaxation period, the post experiment idle conditions are applied to the cell and the instrument returns to the idle state.
Current is plotted as a function of the potential applied to the working electrode, resulting in a voltammogram.
The parameters for this method are arranged on various tabs on the setup panel. The most commonly used parameters are on the Basic tab, and less commonly used parameters are on the Advanced tab. Additional tabs for Ranges and post experiment idle conditions are common to all of the electrochemical techniques supported by the AfterMath software.
You can click on the “I Feel Lucky” button (located at the top of the setup) to fill in all the parameters with typical default values. You will no doubt need to change the Initial Potential, Final Potential, and Sweep Rate to values which are appropriate for the electrochemical system being studied.
The Basic tab contains the same parameters as CV or LSV plus a Speed parameter (see Figure 1). This is because RDE is typically treated as a steady-state CV or LSV experiment. Please see the Theory section below for a more thorough description. If you choose one segment, you must enter the Initial potential, Final potential, Sweep rate, and rotator Speed.
Figure 1: Basic tab setup for one segment RDE
If you choose two segments, then you need to enter the Initial potential, Vertex potential, Final potential, Sweep rate, and rotator Speed. (see Figure 2).
Figure 2: Basic tab setup for two segment RDE
The Electrode Range on the Basic tab is used to specify the expected range of current. If the choice of electrode range is too small, actual current may go off scale and be truncated. If the electrode range is too large, the voltammogram may have a noisy, choppy, or quantized appearance. Please see the ugly duckling page for more information.
Some Pine potentiostats (such as the WaveNow and WaveNano portable USB potentiostats) have current autoranging capability. To take advantage of this feature, set the electrode range parameter to “Auto”. This allows the potentiostat to choose the current range “on-the-fly” while the voltammogram is being acquired.
The actual waveform that is applied to the electrode is linear but not truly analog (see Figure 3A). The flat portions at the beginning and end of the waveform are the induction and relaxation periods, respectively. A typical two segment sweep starts at an initial potential, sweeps to a vertex potential, and then returns to a final potential. The sweep is not perfect; in reality is consists of many small steps (see Figure 3B, black trace, sweep rate ) which are generated using the maximum available resolution of the potentiostat's digital-to-analog converter (DAC).
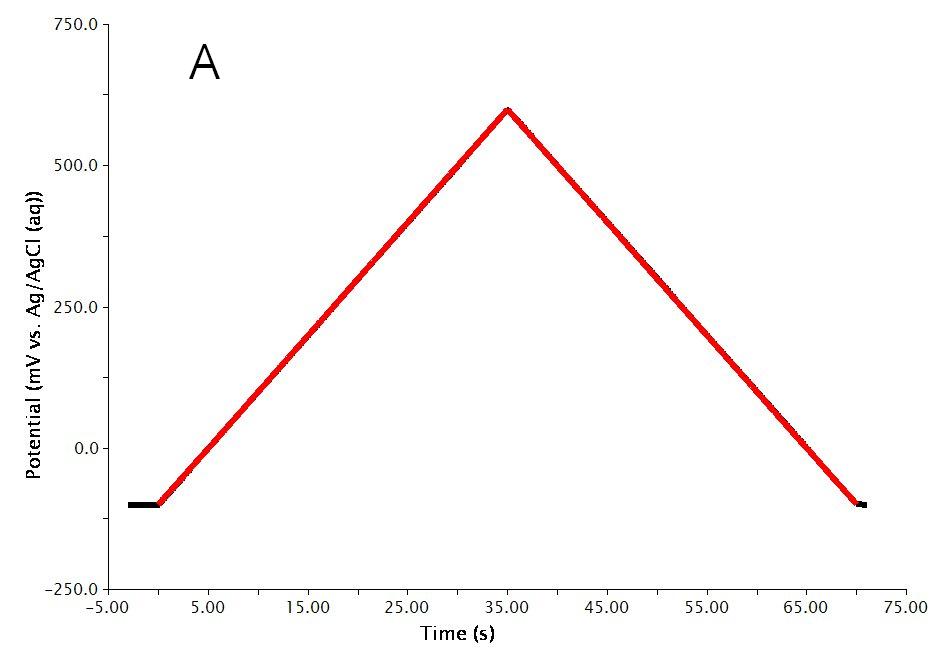
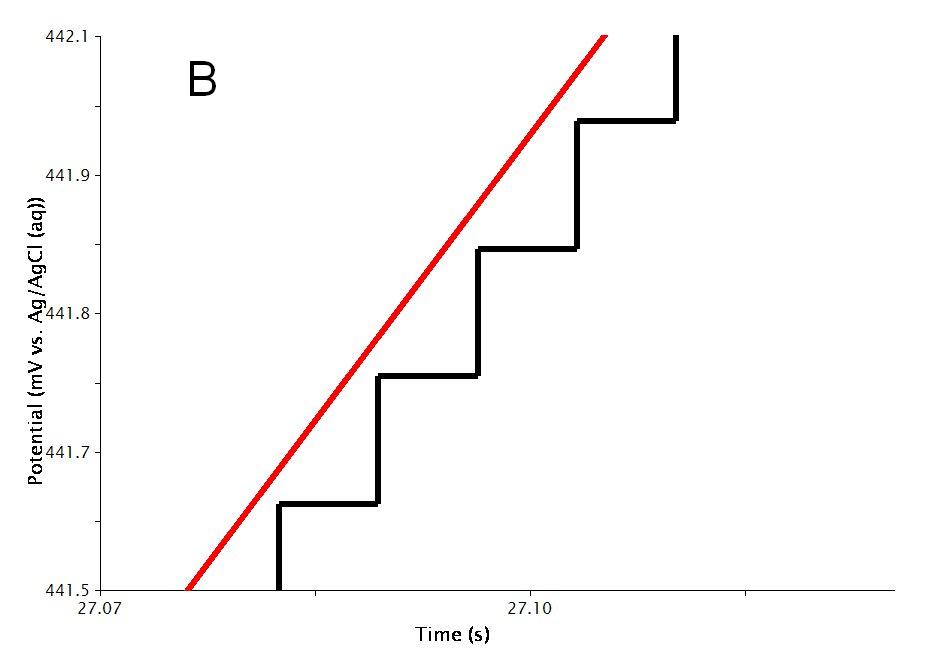
Figure 3: Two Segment RDE Waveform Details of A) the Total Waveform and B) a Magnified Waveform showing the Stepped, Applied Potential (black) and Measured Potential (red)
While RDE typically consists of one or two segments it is possible to choose any number of segments. If you choose any odd number of segments greater than two (see Figure 4), the parameters that must be entered are a little different than the two segment case. You must choose an Initial Potential, Upper Potential, Lower Potential, and Final potential. You must also choose whether the Initial direction is rising (sweep towards Upper Potential) or falling (sweep towards Lower Potential). If the Initial direction is rising, the Final potential must be different than the Lower potential. If the Initial direction is falling, the Final potential must be different than the Upper potential.
Figure 4: Basic tab setup for three segment RDE
If you choose any even number of segments greater than two (see Figure 5) the parameters that must be entered are the same as the three segment case. You must choose an Initial Potential, Upper Potential, Lower Potential, and Final potential. You must also choose whether the first sweep is initially rising (sweep towards Upper Potential) or falling (sweep towards Lower Potential). If the Initial direction is rising, the Final potential must be different than the Upper potential. If the Initial direction is falling, the Final potential must be different than the Lower potential.
Figure 5: Basic tab setup for four segment RDE
The Advanced Tab for this method (see Figure 6) allows you to change the behavior of the potentiostat during the induction period and relaxation period. By default, the potential applied to the working electrode during the induction and relaxation period will match the initial potential and final potential, respectively, as specified on the Basic Tab. You may override this default behavior, and you may also change the durations of the induction and relaxation periods if you wish.
Other important parameters on the Advanced tab are found in the Sampling Control area. This area contains two parameters, Alpha and Threshold which control when and how samples are acquired during the sweep portion of the experiment.
Figure 6: Advanced parameters for RDE
As mentioned previously, the waveform applied to the electrode (see Figure 3) is not truly linear. The actual waveform is a staircase of small potential steps. The duration of each small step is called the step period, and the step period is automatically chosen to take full advantage of the resolution of the potentiostat's digital-to-analog converter.
The Alpha parameter controls the exact time within the step period at which the current is sampled. A alpha value of zero means the current is sampled at the start of the step period, immediately after a new potential step is applied. An alpha value of 100 means the current is sampled at the end of the step period, immediately before the next potential step is applied.
Changing alpha will have little effect on the voltammogram for a freely diffusing species in solution; however, variations in alpha can dramatically influence the results for surface bound species, especially when using older potentiostats with low DAC resolution (i.e., 12-bit).
Newer potentiostats (such as the WaveNow and WaveNano portable USB potentiostats) have 16-bit DAC resolution, so voltammograms acquired using these instruments are less influenced by the choice of alpha value. Nevertheless, researchers who use digital potentiostats to study surface-confined electrochemical systems (rather than freely diffusing species in solution) should be aware of the influence of this parameter. Further details can be found in the literature1 and in a related article about CBP Bipotentiostat Interface Boards.
The Threshold parameter helps you to limit the amount of data retained as the voltammogram is acquired. The threshold parameter controls the interval between samples as the potential is swept from one limit to another. By default, a data point is acquired every time the sweep moves 5 millivolts. You can change the threshold from 5 millivolts to a smaller interval (if you want to acquire more data) or to a greater interval (if you want to acquire less data).
Extreme values for the threshold parameter can lead to undesirable results (see Figure 7 of cyclic voltammetry). A very small Threshold value will produce smooth curves yet results in large files. A very large value though, results in jagged curves.
AfterMath has the ability to automatically select the appropriate ranges for voltage and current during an experiment. However, you can also choose to enter the voltage and current ranges for an experiment. Please see the separate discussions on autoranging and the Ranges Tab for more information.
After the Relaxation Period, the Post Experiment Conditions are applied to the cell. Typically, the cell is disconnected but you may also specify the conditions applied to the cell. Please see the separate discussion on post experiment conditions for more information.
The typical results for a one electrode reversible redox process is a sigmoidal shaped voltammogram (see Figure 7, specific parameters were: Ferrocene in
,
Pt disk,
,
).
Figure 7: Rotating Disk Voltammogram of a Ferrocene Solution
The limiting current can be obtained from the voltammogram by right clicking on the trace and selecting “Add Tool » Peak Height” (see Figure 8, specific parameters were: Ferrocene in
,
Pt disk,
,
). The peak height that is initially drawn (see Figure 9, specific parameters were identical to Figure 8) may have to be changed to properly measure the limiting current.
Figure 8: Addition of Peak Height Tool to Measure Limiting Current
Figure 9: Peak Height Tool Added
By dragging the control points on the tool around you can draw a proper baseline (see Figure 10).
Figure 10: A Proper Baseline for Measurement of the Limiting Current
The baseline type that is initially chosen typically does a good job for a one component reversible system such as that shown above. However, you can change the baseline type by right clicking on the tool and selecting “Properties” (see Figure 11).
Figure 11: Selection of Baseline Properties
This will bring up a dialog box where you can select the type of baseline from the drop-down menu (see Figure 12).
Figure 12: Dialog Box Showing Baseline Types
A series of rotation speeds was used to examine the Ferrocene solution mentioned above (see Figure 13). The limiting current for a freely diffusing species in solution is proportional to the square root of the rotation speed (see Figure 13, inset).
Figure 13: Effect of varying the rotation speed for a Ferrocene Solution from 300 – 2500 rpm. Inset: Plot of Limiting Current versus Square Root of Rotation Speed.
Typical sweep rates are . As long as the system being studied remains in steady-state conditions, sweep rate will have no effect on the limting current. When sweep rates get fast, voltammograms obtained begin to look like typical cyclic voltammograms where the electrode is not rotated. This is due to depletion of the Levich layer of the species being oxidized or reduced. As an example, there is no difference between
and
sweep rates for a
Ferrocene solution when the rotator speed is
(see Figure 14, Black trace =
(underneath Red trace), Red trace =
, Blue trace =
, Green trace =
). However, when the sweep rate is
or
, the voltammograms show signs of depletion of the Levich layer and begin to resemble voltammograms seen in traditional CV. Please see the Theory section for more details if necessary.
Figure 14: Effect of varying the Sweep Rate for a Ferrocene Solution.
The following theoretical introduction to RDE is intended to give the reader a general understanding so that they may better understand what parameters affect the outcome in a typical experiment. A more detailed description can be found in Bard and Faulkner.2 Rotating the electrode is a method of forced convection with the purpose of continually delivering material to the electrode in a controlled manner. The rotating rod creates a vortex flow underneath the electrode which pulls material upwards.
The purpose of rotating the electrode is to keep the solution homogeneous. However, next to the electrode is a stagnant layer, called the Levich layer which actually “clings” to the electrode and rotates with it. Inside this layer, the primary mode of mass transport is diffusion. Even though the primary mode of mass transport is diffusion like in cyclic voltammetry, linear sweep voltammetry, or chronoamperometry the concentration gradient at the electrode remains constant with respect to time. Since the concentration gradient remains constant with respect to time, the current is a steady-state current.
The thickness of the Levich layer will depend upon the experimental conditions and is governed by the equation
where is the diffusion coefficient (in
),
is the rotation speed (
), and
is the kinematic viscosity (in
, see Table 1).
| Table 1: Kinematic Viscosities for |
|
| Solution | |
| |
|
| |
|
| |
|
| |
|
| Pyridine | |
| |
|
| N,N-Dimethylacetamide | |
| |
|
| |
|
The limiting current at electrode is proportional to the thickness of the Levich layer and is defined by
where is the number of electrons in the electrochemical reaction,
is Faraday's constant (
),
is the electrode area (in
), and
is the concentration (in
). Finally, the fully expanded limiting current is defined by the Levich equation,
.
In the first example, Gallaway and Barton3 coated an electrode with an oxygen-reducing enzyme and a series of redox-polymers. The purpose of this was to examine mediated electron transfer in a biocatalyzed fuel cell. Varying the type of redox-polymer used, the researchers were able to examine rate constants as a function of overpotential between the enzyme and mediator. These data were then used to determine the optimum polymer redox potential in order to get maximum power output for a hypothetical biofuel cell.
The next example uses RDE to examine the reduction of ferricyanide, in the prescence of methylene blue (MB), at a DNA-modified electrode. Boon et al.4 used a gold-disk electrode that was modified with self-assembled monolayers of a double-stranded oligonucleotide selective for the adsorption of MB. The rate limiting step was determined, from RDE, to be the adsorption of MB onto the electrode. Despite slow sweep rates, the resulting voltammograms showed interesting “peak-shaped” i-V traces that took several seconds to reach their steady-state values. These “peak-shaped” traces were attributed to the slow transfer of MB into and out of the film.
The third example, Orilall et al.5 synthesized Pt and Pt-Pb nanoparticles and incorporated them into mesoporous niobium-oxide/carbon composites. Heat treating this composite made a graphitic-like material that was assembled onto a glassy carbon disk electrode. The researchers investigated this material for formic acid oxidation and found that it had a four times higher mass activity and lower onset potential than any previously reported Pt-Pb nanoparticles.
In the fourth example, Zhang et al.6 used RDE to examine the reduction of oxygen. Multiwalled carbon nanotubes (MWCNTs) were functionalized with a Co-porphyrin complex and then mixed with Nafion. This material was then dropcast onto a glassy carbon disk electrode. RDE was then used to show that the mechanism for oxygen reduction was a direct four-proton and four-electron reduction of oxygen to water. These results showed that the materials would be a suitable substitute for platinum or other metal-based cathode materials in proton conducting membrane fuel cells.
The fifth example uses RDE to examine the mechanism of electrochemical reduction of H2O2 on Cu in acidic sulfate solutions. Stewart and Gerwith7 studied the interaction of H2O2 with Cu because H2O2 is commonly used as an oxidizer component in chemical mechanical planarization (CMP) slurries. CMP is used in microelectronics applications. By using RDE, the researchers were able formulate a mechanism that involved a never observed before Cu(I) intermediate following peroxide exposure. The researchers went on to use other techniques to look for and find this Cu(I) intermediate.
The final example shows how RDE can be used in a teaching lab for advanced undergraduate or first-year graduate chemistry or chemical engineering labs. Kear et al.8,9 use Cu disk electrodes in aerated sea water to examine the reduction of oxygen at a cathode surface. This is a way to introduce electrochemical engineering and corrosion to students and is informative in explaining cathodic kinetics in corrosion reactions. The students also used this experiment as a hand-on approach to learning about mass transfer since the examination of the limiting current at various rotation speeds allows for the calculation of the diffusion coefficient for oxygen.
1. He, P. Anal. Chem., 1995, 67, 986-992.
2. Faulkner, L. R.; Bard, A. J. Methods Involving Forced Convection – Hydrodynamic Methods, Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New Jersey, 2000; 331-367.
3. Gallaway, J. W.; Barton, S. A. C. J. Am. Chem. Soc., 2008, 130, 8527–8536.
6. Zhang, W.; Shaikh, A. U.; Tsui, E. Y.; Swager, T. M. Chem. Mater., 2009, 21, 3234–3241.
7. Stewart, K. L.; Gewirth, A. A. Langmuir, 2007, 23, 9911–9918.
8. Chemical Engineering Education
9. Kear, G.; A. P.-de-L., C.; Walsh, F. C. Chem. Eng. Ed., 2005, 39, 14-21.

Request a Quote for this Cart
Below is the billing data we have on file. These details will be used on your quotation, so please update them here if you require any changes. Changing any details here updates them for your account.













