This article is part of the AfterMath Data Organizer Electrochemistry Guide
Detailed Description
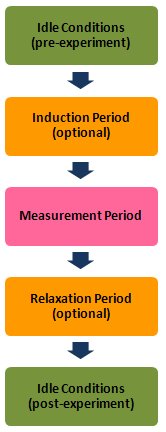
Like most of the other electrochemical techniques offered by the AfterMath software, this experiment begins with an induction period. During the induction period, a set of initial conditions is applied to the electrochemical cell and the cell is allowed to equilibrate to these conditions. The default initial condition involves holding the working electrode potential at the Initial Potential for a brief period of time (i.e., 3 seconds).
After the induction period, the potential of the working electrode is stepped to a specified potential for a period of time.
After the first step has finished, the potential of the working electrode is stepped back for a specified period of time, usually to the potential prior to the forward step. The experiment concludes with a relaxation period. The default condition during the relaxation period involves holding the working electrode potential at the initial potential for an additional brief period of time (i.e., 1 seconds).
At the end of the relaxation period, the post experiment idle conditions are applied to the cell and the instrument returns to the idle state.
Current is plotted as a function of time, resulting in a chronoamperogram. You may also choose to do some post experiment processing in order to generate Cottrell plots.
Parameter Setup
The parameters for this method are arranged on various tabs on the setup panel. The most commonly used parameters are on the Basic tab which is similar to that for CA with the addition of a Reverse step period box. Additional tabs for Ranges and Post Experiment Conditions are common to all of the electrochemical techniques supported by the AfterMath software. Finally, a Post Experiment Processing tab deals with manipulating the data automatically when the experiment is finished.
Basic Tab
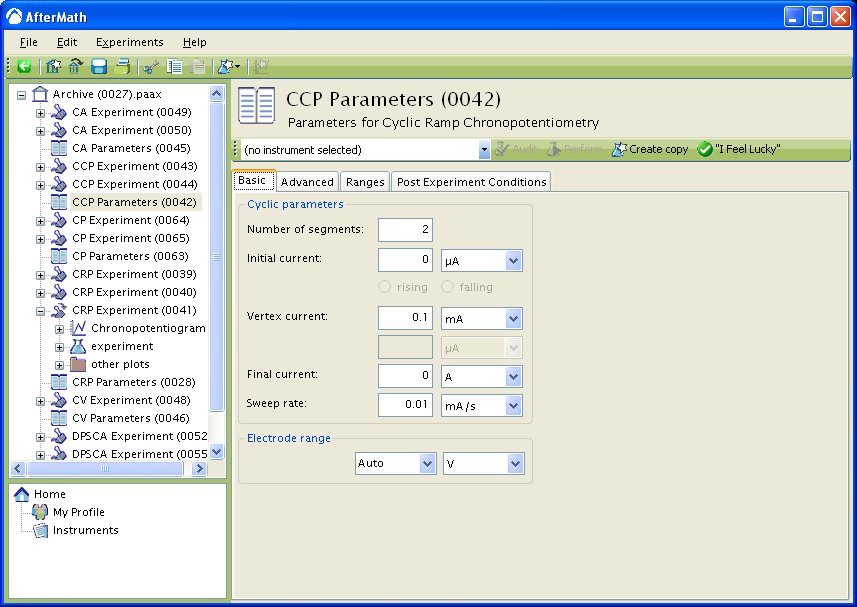
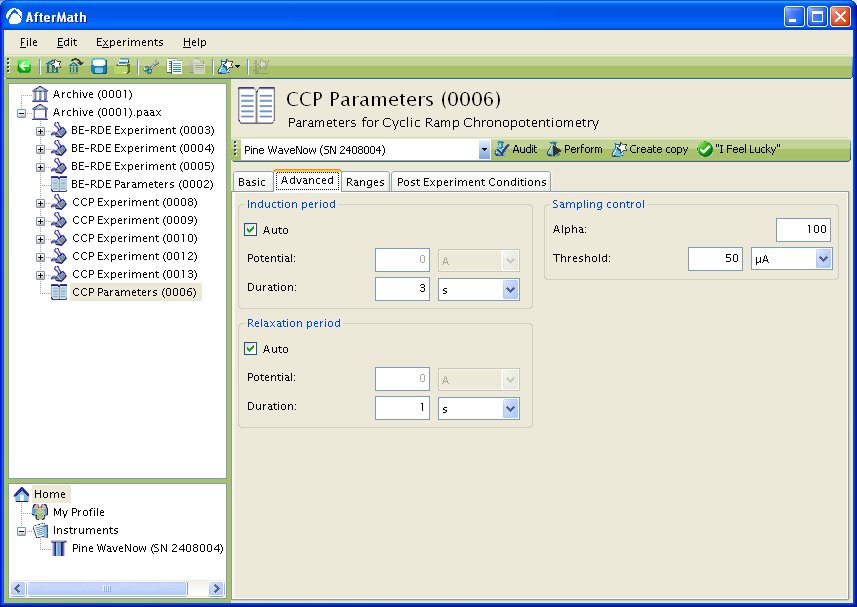
You can click on the “I Feel Lucky” button (located at the top of the setup) to fill in all the parameters with typical default values (see Figure 1). You will no doubt need to change the Potential and Hold time in the Forward step period and Reverse step period boxes to values which are appropriate for the electrochemical system being studied. You may also want to change the Number of intervals in the Sampling Control box.
Figure 1: Basic Setup for Double Potential Step Chronoamperometry.
The Electrode K1 Current Range on the Basic tab is used to specify the expected range of current. If the choice of electrode range is too small, actual current may go off scale and be truncated. If the electrode range is too large, the chronoamperogram may have a noisy, choppy, or quantized appearance.
Some Pine potentiostats (such as the WaveNow and WaveNano portable USB potentiostats) have current autoranging capability. To take advantage of this feature, set the electrode range parameter to “Auto”. This allows the potentiostat to choose the current range “on-the-fly” while the chonoamperogram is being acquired.
The waveform that is applied to the electrode is a simple pulse to the Potential listed in the Forward step period box for the Hold time followed by a step back to the Potential specified in the Reverse step period box. Note that the actual waveform that is measured (see Figure 2, red trace) fluctuates slightly compared to the applied potential (see Figure 2, black trace).
Figure 2: Waveform for DPSCA. Black = applied potential, Red trace = measured potential.
Ranges Tab
AfterMath has the ability to automatically select the appropriate ranges for voltage and current during an experiment. However, you can also choose to enter the voltage and current ranges for an experiment. Please see the separate discussions on autoranging and the Ranges Tab for more information.
Post Experiment Conditions Tab
After the Relaxation Period, the Post Experiment Conditions are applied to the cell. Typically, the cell is disconnected but you may also specify the conditions applied to the cell. Please see the separate discussion on post experiment conditions for more information.
Post Experiment Processing Tab
The Post Experiment Processing Tab (see Figure 3) looks similar to that for CA and allows you to automatically generate Cottrell current, Cottrell charge, DPSCA working curve, or DPSCC working curve plots. Please see the Typical Results and Theory sections of this wiki for more information regarding Cottrell plots and DPSCA/DPSCC working curves.
Figure 3: Post Experiment Processing Options.
Typical Results
The results for a solution of Ferrocene in
are shown in Figure 4. Specific conditions include the use of a
Pt WE, forward step potential of
and reverse step potential of
.
Figure 4: Double Potential Step Chronoamperogram of a Ferrocene Solution
If you selected to automatically generate Cottrell plots, the plots are under the other plots folder in the Archive navigation panel. Choosing Cottrell current displays a plot of current versus the (see Figure 5A). Choosing Cottrell charge displays a plot of charge versus
(see Figure 5B). Note that for the Cottrell Current plot, the level portion in the plot is actually the time prior to the current spike shown in Figure 4. That is, earlier time points are to the right in a Cottrell Current Plot. This is not the case for a Cottrell Charge plot because integrating the current with respect to time gives charge.
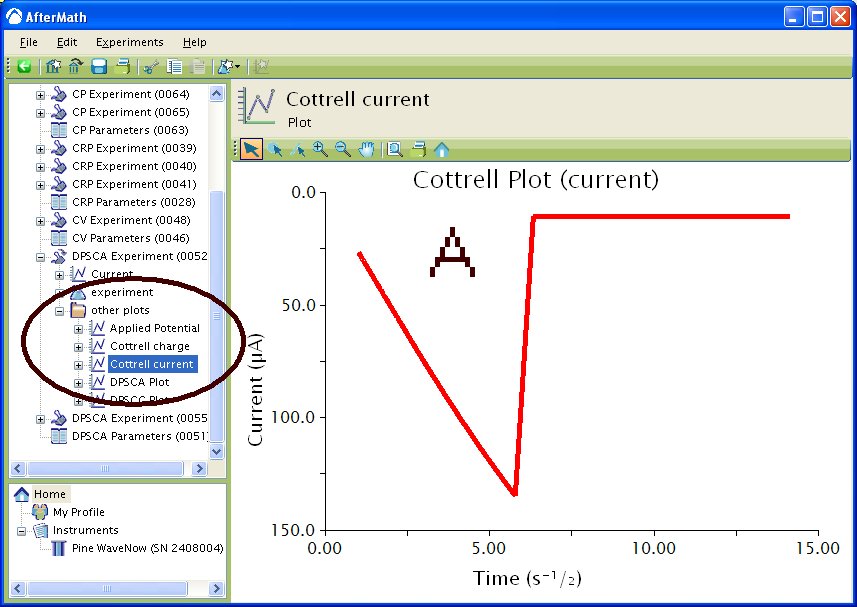
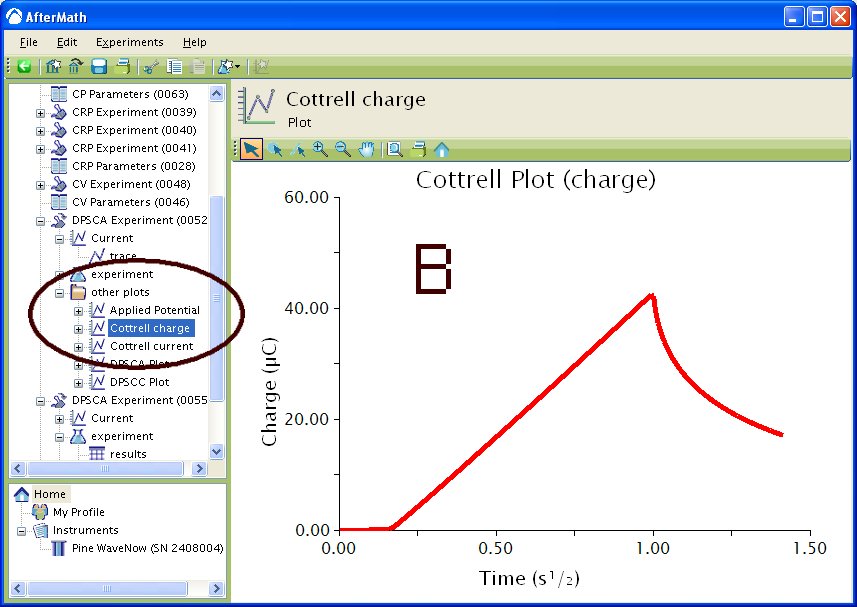
Figure 5 : Post experiment processing plots. A – Cottrell Current, B – Cottrell Charge. Conditions as listed in Figure 4.
If you selected to automatically generate DPSCA or DPSCC working curves, they are also under the other plots folder in the Archive navigation panel. The theory for the forward step in DPSCA is the same as the theory for the first step in CA, however the theory for the reverse step is complicated by the first step. The DPSCA working curve (see Figure 6) is a useful way to examine if kinetic complications of the redox species are present. If there are no kinetic complications and both potential steps are to regions of diffusion-limited currents, the actual (see Figure 6, red trace) working curve will overlay the ideal (see Figure 6, black trace) working curve. The ideal working curve is theoretically generated according to the equation
where is the reverse current at
,
is the forward current at
and
. A quick check for a stable system is:
Figure 6: DPSCA Working Curve. Actual = red trace, Ideal = black trace. Conditions as listed in Figure 4.
The DPSCC working curve (see Figure 7) is a useful way to examine the charge passed during an experiment and is similar to the Cottrell Charge plot except that it separates the forward (see Figure 7, red trace) and reverse (see Figure 7, black trace) steps. The reverse step is corrected to account for the charge passed during the forward step, making the charge passed in the reverse step linear with respect to time.
Figure 7 : DPSCC Working Curve. Forward – red trace, Reverse – black trace. Conditions as listed in Figure 4.
Theory
As stated in the Theory section of CA, the time-dependent current transient in a diffusion-limited chronoamperometry experiment is governed by the Cottrell2 equation
where is the number of electrons,
is Faraday's Constant (
),
is the electrode area (
),
is the diffusion coefficient (
), and
is the concentration (
). In DPSCA, the time of the transition must be taken into account. The current transient for the second pulse, provided it produces diffusion-limited currents, is governed by the equation first obtained by Kambara3
where is the transition time and the other parameters are as above. Dividing the reverse current at time
by
and keeping
allows for the generation of a working curve given by the equation
If there are no kinetic complications in the electrode reaction, the actually working curve should fall on an ideal working curve as shown in Figure 6. Note that the deviation at the beginning of the working curve is due to the electronics of the potentiostat.
DPSCA is a technique that is often used to elucidate mechanisms related to coupled homogeneous reactions preceeding or following an electrode reaction. Bard and Faulkner1 give a more detailed description of using DPSCA to elucidate mechanisms. A brief description will be given here as to what types of mechanisms can be elucidated and how you might apply DPSCA. Several examples are listed in the Application section also.
The simplest coupled homogeneous reactions are Electrochemical-Chemical (EC) and Chemical-Electrochemical (CE).
Application
This example uses DPSCA to calculate the diffusion coefficients for a subtrate () and a product (
) of an electrode reaction. Hyk et al.4 examined the current transients for DPSCA to analyze the reaction
. The researchers generated equations for dealing with both hemispherical electrodes and disk microelectrodes under diffusion-limited and mixed diffusion-migration. Interestingly, the researchers were able to show that for an uncharged substrate with less than
supporting electrolyte they are able to obtain diffusion coefficients. This is significant because an uncharged substrate with less than 0.1% supporting electrolyte does not lend to calculation of diffusion coefficients by single potential step chronoamperometry.
In this next example, Long et al.5 used a slight variant of DPSCA to examine diffusion and self-exchange in a cobalt bipyridine redox polyether hybrid. Films of material, containing supporting electrolyte, were prepared on inter-digitated array electrodes (IDAs). A pulse was generated (equivalent to a double-potential step) on one set of fingers on the IDA while the current was monitored on the second set of fingers on the IDA. Monitoring the time it takes for the pulse to travel from the generator set of fingers to the collector set of fingers allowed for the calculation of diffusion coefficients and self-exchange rate constants between metal centers.
In the final example, Schwarz and Shain6 used DPSCA to measure the rate constant for a chemical reaction after an electrochemical reaction, commonly referred to as an EC reaction. The overall reaction for the general process is
where the product is electrochemically inactive. In this example, the researchers reduce azobenzene to hydrazobenzene which in turn rearranges to benzidine in acidic solutions. By varying the time of the second step, the researchers were able to determine the rate constant for the reaction of hydrazobenzene rearrangning to benzidine.
References
1. Faulkner, L. R.; Bard, A. J. Basic Potential Step Methods, Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New Jersey, 2000; 156-225.
2. Cottrell, F. G. Z. Physik, Chem., 42, 1902, 385.
3. Kambara, T. Bull. Chem. Soc. Jpn., 1954, 27, 523.
4. Hyk, W; Nowicka, A.; Stojek, Z. Anal. Chem., 2002, 74, pp 149–157.
5. Long, J. W.; Terrill, R. H.; Williams, M. E.; Murray, R. W. Anal. Chem., 1997, 69, pp 5082–5086.
6. Schwarz, W. M.; Shain, I. J. Phys. Chem., 1965, 69, pp 30-40.
Additional Resources
Links: Electrochemist's Guide, AfterMath User's Guide, AfterMath Main Support Page
Related Techniques: Chronoamperometry (CA)
Read More
Experimental Considerations

This article is part of the AfterMath Data Organizer Electrochemistry Guide
Interdependency of the Potentiostat and Electrochemical Cell
One of the key aspects of electrochemical measurements is that the potentiostat and the electrochemical cell are part of the same electrical circuit. If something is wrong with the cell, then the cell can make the potentiostat appear to have a problem. Or, if something is wrong with the potentiostat, it can cause an unwanted change to occur within the cell. Other kinds of laboratory instrumentation, from the lowly digital balance to more complex spectrophotometers and chromatographic detectors, are relatively immune to changes in the nature of the sample being analyzed and are less likely to cause unwanted changes in the composition of the sample. But the successful user of a potentiostat must always be aware of the significant interdependence between the potentiostat and the sample and plan experiments accordingly.
Part of this awareness is carefully managing the sequence of events before, during, and after an electroanalytical measurement. The initial conditions imposed upon an electrochemical cell (such as the working electrode potential) as well as the instrument settings (such as the current range) can have a direct bearing on the observed results of an electrochemical measurement. Similarly, the continuity of cell control (or lack thereof) after a measurement concludes can directly influence the composition of the portions of the electrochemical cell immediately adjacent to the electrode(s). Indeed, the surface properties of the electrodes themselves can be unwittingly altered by improper cell control.
Minimizing Cell Change for a Successful Electroanalytical Measurement
A strategy for a successful electroanalytical measurement often begins with devising a way to connect the electrodes to the potentiostat without any appreciable changes occurring within the cell. In the jargon of the electroanalytical chemist, this might be as simple as initially poising the working electrode at a potential where no Faradaic current flows. Or, in the jargon of the corrosion scientist, it might be wise to start an experiment with the corrosion sample at or near OCP (Open Circuit Potential, the potential at which there is no current at the working electrode).
The AfterMath software gives you control of the idle conditions which prevail while you are making electrode connections and before an experiment begins. These “pre-experiment” idle conditions can be adjusted at any time while the potentiostat is not doing an experiment. You can choose to hold the working electrode at a given potential under potentiostatic control or alternately, at a given current (usually zero amperes) under galvanostatic control. You may also choose to hold the electrode at OCP if you wish.
Click here for more information about adjusting pre-experiment idle conditions.
The Induction Period
As part of the experimental specifications for an electrochemical technique, AfterMath allows you to specify a period of time during which the cell is allowed to come into equilibrium with the initial signal levels applied to the working electrode(s). The period of time, called the induction period, is brief by default (usually less than 3 seconds); however, you may increase the duration of the induction period or you may skip the induction period if you wish.
Click here for more information about setting up the induction period.
Idle Conditions

This article is part of the AfterMath Data Organizer Electrochemistry Guide
During the time period between experiments, it is usually important to assure that conditions of the electrochemical cell do not allow any unwanted electrochemical processes to occur. A passive approach is to merely disconnect the cell from the instrument (either manually or automatically) and prevent any stray currents in the cell. A more active approach is to keep the cell connected to the instrument and carefully apply the appropriate signal levels to the electrode(s) to prevent any redox processes.
The AfterMath software allows you to control and monitor the condition of the electrochemical cell at any time when the instrument is idle. This control is provided by clicking on the instrument in the Instrument List and viewing the Instrument Status (see below). One of the tabs on the Instrument Status panel is the “Idle” tab. This tab has cell and electrode controls (top half) and also indicators showing cell status (bottom half).
In the example above, the first working electrode is set to a passive mode of operation (open circuit potential). In the status area (bottom half), you can see that the OCP level is and the current has a magnitude of about
. In addition to the passive OCP mode of operation, you may choose three other modes of operation for an electrode: potentiostatic, galvanostatic, and zero-resistance ammeter (ZRA). When a working electrode idles in one of the two active states (potentiostatic or galvanostatic), then you may choose the signal level that is to be actively applied to the electrode. (see below).
In the example above, the first working electrode is idling in potentiostatic mode, and there is no control of any second working electrode (because the Pine WaveNow potentiostat does not support a second working electrode). The setpoint for the first working electrode potential is . The actual potential of the first working electrode is monitored in real time in the status area (bottom half) on the Idle tab. You can see that in this example the “live potential” at the first working electrode is actually
and the “live current” is
.
NOTE: The availability of the four modes of operation (potentiostatic, galvanostatic, OCP, and ZRA) depends upon the particular instrument model that you are using. Not all instruments support all four modes of operation on all electrodes.
Links: Electrochemist's Guide, AfterMath User's Guide, AfterMath Main Support Page
Related Topics: post-experiment idle conditions, cell switching
Cyclic Voltammetry (CV)

This article is part of the AfterMath Data Organizer Electrochemistry Guide
Detailed Description
Like most of the other electrochemical techniques offered by the AfterMath software, this experiment begins with an induction period. During the induction period, a set of initial conditions is applied to the electrochemical cell and the cell is allowed to equilibrate to these conditions. The default initial condition involves holding the working electrode potential at the Initial Potential for a brief period of time (i.e., 3 seconds).
After the induction period, the potential of the working electrode is swept linearly at the specified Sweep Rate to a Vertex Potential. Upon reaching the vertex potential, the direction of the sweep is reversed, and the sweep continues back to a Final Potential.
After the sweeping has finished, the experiment concludes with a relaxation period. The default condition during the relaxation period involves holding the working electrode potential at the final potential for an additional brief period of time (i.e., 1 seconds).
At the end of the relaxation period, the post experiment idle conditions are applied to the cell and the instrument returns to the idle state.
Current is plotted as a function of the potential applied to the working electrode, resulting in a voltammogram.
Parameter Setup
The parameters for this method are arranged on various tabs on the setup panel. The most commonly used parameters are on the Basic tab, and less commonly used parameters are on the Advanced tab. Additional tabs for Ranges and post experiment idle conditions are common to all of the electrochemical techniques supported by the AfterMath software.
Basic Tab
You can click on the “I Feel Lucky” button (located at the top of the setup) to fill in all the parameters with typical default values. You will no doubt need to change the Initial Potential, Vertex Potential, Final Potential, and Sweep Rate to values which are appropriate for the electrochemical system being studied.
Figure 1: Basic Cyclic Voltammetry Setup
The Electrode Range on the Basic tab is used to specify the expected range of current. Consider performing cyclic voltammetry (using a GC working electrode and sweep rate =
) on a
solution of
in
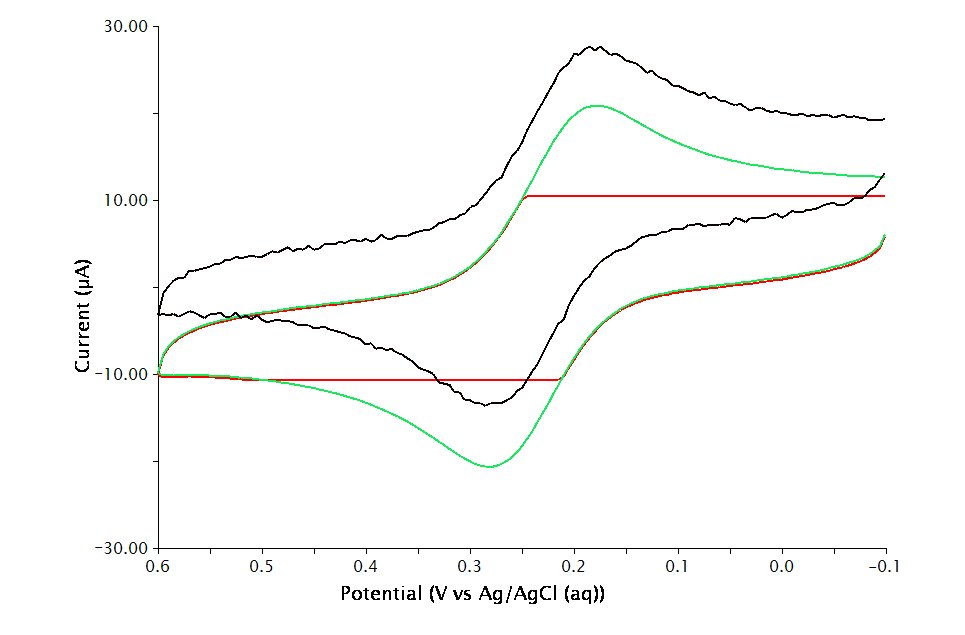
. If the choice of electrode range is too small (e.g.
), actual current may go off scale and be truncated (see Figure 2, red trace). If the electrode range is too large (e.g.
), the voltammogram may have a noisy, choppy, or quantized appearance (see Figure 2, black trace). With the adequate electrode range (e.g.
), the volatammogram has a desirable appearance (see Figure 2, green trace)
Some Pine potentiostats (such as the WaveNow and WaveNano portable USB potentiostats) have current autoranging capability. To take advantage of this feature, set the electrode range parameter to “Auto”. This allows the potentiostat to choose the current range “on-the-fly” while the voltammogram is being acquired.
Figure 2 : Influence of Current Range Choice on Voltammogram Quality
The actual waveform that is applied to the electrode is linear but not truly analog (see Figure 3A). The flat portions at the beginning and end of the waveform are the induction and relaxation periods, respectively. A typical two segment sweep starts at an initial potential, sweeps to a vertex potential, and then returns to a final potential. The sweep is not perfect; in reality is consists of many small steps (see Figure 3B, black trace) which are generated using the maximum available resolution of the potentiostat’s digital-to-analog converter (DAC).
Figure 3: Cyclic Voltammetry Waveform Details: Total waveform (A), Zoom of waveform showing steps (B)
While cyclic voltammograms are typically two segments or one cycle, it is possible to choose any number of segments for an experiment. If you choose any odd number of segments greater than two (see Figure 4), the parameters that must be entered are a little different than the two segment case. You must choose an Initial Potential, Upper Potential, Lower Potential, and Final potential. You must also choose whether the Initial direction is rising (sweep towards Upper Potential) or falling (sweep towards Lower Potential). If the Initial direction is rising, the Final potential must be different than the Lower potential. If the Initial direction is falling, the Final potential must be different than the Upper potential.
Figure 4: Three Segment Cyclic Voltammetry
If you choose any even number of segments greater than two (see Figure 5) the parameters that must be entered are the same as the three segment case. You must choose an Initial Potential, Upper Potential, Lower Potential, and Final potential. You must also choose whether the first sweep is initially rising (sweep towards Upper Potential) or falling (sweep towards Lower Potential). If the Initial direction is rising, the Final potential must be different than the Upper potential. If the Initial direction is falling, the Final potential must be different than the Lower potential.
Figure 5: Four Segment Cyclic Voltammetry
Advanced Tab
The Advanced Tab for this method (see Figure 6) allows you to change the behavior of the potentiostat during the induction period and relaxation period. By default, the potential applied to the working electrode during the induction and relaxation period will match the initial potential and final potential, respectively, as specified on the Basic Tab. You may override this default behavior, and you may also change the durations of the induction and relaxation periods if you wish.
Other important parameters on the Advanced tab are found in the Sampling Control area. This area contains two parameters, Alpha and Threshold which control when and how samples are acquired during the sweep portion of the experiment.
Figure 6: Advanced parameters for Cyclic Voltammetry
As mentioned previously, the waveform applied to the electrode (see Figure 3) is not truly linear. The actual waveform is a staircase of small potential steps. The duration of each small step is called the step period, and the step period is automatically chosen to take full advantage of the resolution of the potentiostat’s digital-to-analog converter.
The Alpha parameter controls the exact time within the step period at which the current is sampled. A alpha value of zero means the current is sampled at the start of the step period, immediately after a new potential step is applied. An alpha value of 100 means the current is sampled at the end of the step period, immediately before the next potential step is applied.
Changing alpha will have little effect on the voltammogram for a freely diffusing species in solution; however, variations in alpha can dramatically influence the results for surface bound species, especially when using older potentiostats with low DAC resolution (i.e., 12-bit).
Newer potentiostats (such as the WaveNow and WaveNano portable USB potentiostats) have 16-bit DAC resolution, so voltammograms acquired using these instruments are less influenced by the choice of alpha value. Nevertheless, researchers who use digital potentiostats to study surface-confined electrochemical systems (rather than freely diffusing species in solution) should be aware of the influence of this parameter. Further details can be found in the literature1 and in a related article about CBP Bipotentiostat Interface Boards.
The Threshold parameter helps you to limit the amount of data retained as the voltammogram is acquired. The threshold parameter controls the interval between samples as the potential is swept from one limit to another. By default, a data point is acquired every time the sweep moves 5 millivolts. You can change the threshold from 5 millivolts to a smaller interval (if you want to acquire more data) or to a greater interval (if you want to acquire less data).
Again, consider performing cyclic voltammetry (using a GC working electrode and sweep rate =
) on a
solution of
in
. Extreme values for the threshold parameter can lead to undesirable results (see Figure 7). A smaller threshold value, typically less than or equal to 5 millivolts, produces smoother curves and larger data files (see Figure 7, red trace, interval =
). If you set the threshold parameter to zero, then the maximum number of data points is acquired (and the size of the resulting data file will be quite large). If you set the parameter to a very large interval (e.g.
), then the number of points acquired will be so small that the voltammogram appears sharp and jagged (see Figure 7, black trace). Intermediate intervals can also be seen in Figure 7 (gold –
, blue =
).
Figure 7: Influence of Sampling Threshold on Voltammogram Quality
Ranges Tab
AfterMath has the ability to automatically select the appropriate ranges for voltage and current during an experiment. However, you can also choose to enter the voltage and current ranges for an experiment. Please see the separate discussions on autoranging and the Ranges Tab for more information.
Post Experiment Conditions Tab
After the Relaxation Period, the Post Experiment Conditions are applied to the cell. Typically, the cell is disconnected but you may also specify the conditions applied to the cell. Please see the separate discussion on post experiment conditions for more information.
A principle result of interest from a cyclic voltammogram is the peak current of the voltammogram. The peak current increases with the sweep rate (see Figure 8, conditions are solution of
in
with sweep rates =
,
,
,
, and
for red, gold, green, blue, and black traces, respectively). The peak current is proportional to the square root of the sweep rate (see Figure 8 insert).
Figure 8: Influence of Sweep Rate on a Cyclic Voltammogram
(inset – current vs square root of sweep rate)
The peak current can be obtained by right-clicking on the trace and selecting Add Tool » Peak Height (see Figure 9). This places a peak measurement tool on the voltammogram (not always in the correct place, see Figure 10), and you can move the position of the peak tool using the control points on the tool.
Figure 9: Initial Placement of Peak Height Tool on Voltammogram
Figure 10: Right-Click to Change the Tool Properties
An important part of measuring the peak current is to use the proper baseline. In general, a small portion of the voltammogram leading up to the peak is used as the baseline. This small portion is extrapolated underneath the peak.
Right-clicking on one of the peak tool’s control points will bring up a dialog box where you can change the properties of the tool (see Figure 11). On this dialog box, there is a drop-down menu where you can choose the type of baseline. In this example, the “Free Sloped” baseline type was used. You can then manipulate the tool to draw the desired baseline and obtain an accurate peak height (see Figure 12).
Figure 11: Selection of Baseline
Figure 12: Extrapolation of Baseline for Peak Height Tool
Theory
A brief summary of the theory of cyclic voltammetry will be covered here. Randles2 and Sevcik3 contributed to the development of the theory for cyclic voltammetry, however, credit for the modern treatment and notation goes to Nicholson and Shain4. Additionally, Bard and Faulkner5 provide a nice summary and description of cyclic voltammetry.
Consider a reaction, , with a formal potential
. If a potential sweep is started sufficiently more positive than
and swept negatively a non-faradaic current will initially flow. As the potential of the electrode approaches
,
begins getting reduced to
creating a concentration gradient and therefore flux (mass transfer) to the surface increases. As
passes
, the concentration of
at the surface of the electrode is nearly zero and mass transfer is at a maximum. The current will begin to tail off as the potential is swept to the vertex potential upon which the sweep is reversed.
The concentration of at the surface of the electrode is now very high and oxidation can proceed once
begins to approach
. An inverse of the process described above happens resulting in a similarly shaped but inverted
curve. Ideally, the peak-to-peak separation for the reduction and oxidation waves should be
for a one-electron electrochemically reversible process. Additionally, the peak height
in amperes
can be described by the Randles-Sevcik equation, shown below,
where is the number of electrons,
is Faraday’s Constant
,
is the electrode area,
is the diffusion coefficient,
is the concentration,
is the universal gas constant
,
is the absolute temperature
and
is the sweep rate. At
, with
in
,
in
,
in
and
in
, the above equation simplifies to
A good rule of approximation is will be appoximately
.
Application
Cyclic voltammetry is used extensively and the following two examples highlight its usefulness.
The first example shows that you can calculate electron transfer rate constants using cyclic voltammetry. The theory for calculating electron transfer rate constants from cyclic voltammetry was originally developed by Nicholson6 but the example here is from more recent work by Weber and Creager7. Ferrocene was irreversibly adsorbed in the form of a self-assembled monolayer to a Au surface using a long-chain alkylthiol. Varying the sweep rates gave increasingly larger values (
, overpotential), with
being the oxidation or reduction peak and
being the formal potential for ferrocene in this system. Rate constants were then calculated from these overpotentials. The authors went on to compare the experimentally obtained voltammograms to theoretically calculated voltammograms and from these were comparisons were also able to obtain reorganization energies.
In the second example, Duah-Williams and Hawkridge used cyclic voltammetry to study the temperature dependence of the kinetics of dissociation from the cyanomyoglobin complex (
)8. By comparing the experimentally obtained cyclic voltammograms to theoretically calculated cyclic voltammograms, they were able to estimate the dissociation rate,
, by varying the sweep rate and monitoring the disappearance of an oxidation wave, associated with
as
dissociated. This is a good example of how cyclic voltammetry can give information, such as a dissociation constant, that has been traditionally been measured by NMR.
References
1. He, P. Anal. Chem., 1995, 67, 986-992.
2. Randles, J. E. B.; Trans. Faraday Soc., 1948, 44, 327-338.
3. Sevcik, A. Coll. Czech. Chem. Commun., 1948, 13, 349-377.
4. Nicholson, R. S.; Shain, I. Anal. Chem., 1964, 36, 706-723.
5. Faulkner, L. R.; Bard, A. J. Potential Sweep Methods, Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New Jersey, 2000; 226-260.
6. Nicholson, R. S. Anal. Chem., 1965, 37, 1351-1355.
7. Weber, K.; Creager, S. E. Anal. Chem., 1994, 66, 3164-3172.
8. Duah-Williams, L.; Hawkridge, F. M. J. Electroanal. Chem. 1999, 466, 177-186.
Additonal Resources
Links: Electrochemist’s Guide, AfterMath User’s Guide, AfterMath Main Support Page
Related Techniques: Linear Sweep Voltammetry (LSV), Staircase Voltammetry (SCV)
Differential Pulse Voltammetry (DPV)

This article is part of the AfterMath Data Organizer Electrochemistry Guide
Detailed Description
Like most of the other electrochemical techniques offered by the AfterMath software, Differential Pulse Voltammetry (DPV) begins with an induction period. During the induction period, a set of initial conditions is applied to the electrochemical cell and the cell is allowed to equilibrate to these conditions. The default initial condition involves holding the working electrode potential at the Initial Potential for a brief period of time (i.e., 3 seconds).
After the induction period, the potential of the working electrode is stepped from the Initial potential to the Final potential. The forward step is determined by the Step height and the reverse step is determined by subtracting the Step increment from the Step height. Cyclic Differential Pulse Voltammetry (CDPV) is a variant where the potential of the working electrode is cycled between an Upper baseline potential and a Lower baseline potential.
After the pulse sequence has finished, the experiment concludes with a relaxation period. The default condition during the relaxation period involves holding the working electrode potential at the final potential for an additional brief period of time (i.e., 1 seconds).
At the end of the relaxation period, the post experiment idle conditions are applied to the cell and the instrument returns to the idle state.
Differential current is plotted as a function of the potential applied to the working electrode, resulting in a voltammogram.
Parameter Setup
The parameters for this method are arranged on various tabs on the setup panel. The most commonly used parameters are on the Basic tab, and less commonly used parameters are on the Advanced tab. Additional tabs for Ranges and post experiment idle conditions are common to all of the electrochemical techniques supported by the AfterMath software.
Basic Tab
For DPV, you can click on the “I Feel Lucky” button (located at the top of the setup) to fill in all the parameters with typical default values (see Figure 1). You may need to change the Initial baseline potential and Final baseline potential, to values which are appropriate for the electrochemical system being studied.
Figure 1: Basic setup tab for DPV.
For CDPV, you can click on the “I Feel Lucky” button (located at the top of the setup) to fill in all the parameters with typical default values (see Figure 2). You may need to change the Number of segments, Initial baseline potential, Upper baseline potential, Lower baseline potential and Final baseline potential, to values which are appropriate for the electrochemical system being studied. The Final baseline potential is greyed out for the two segment case.
Figure 2: Basic setup tab for CDPV.
Though two segments would be typical for CDPV, it is possible to choose any number of segments for an experiment. If you choose any odd number of segments greater than two, the parameters that must be entered are a little different than the two segment case. You must choose an Initial baseline potential, Upper baseline potential, Lower baseline potential, and Final baseline potential. You must also choose whether the Initial direction is rising or falling . If the Initial direction is rising, the Final baseline potential must be different than the Lower baseline potential. If the Initial direction is falling, the Final baseline potential must be different than the Upper baseline potential.
If you choose any even number of segments greater than two the parameters that must be entered are the different from the two segment case. You must choose an Initial baseline potential, Upper baseline potential, Lower baseline potential, and Final baseline potential. You must also choose whether the Initial direction is rising or falling . If the Initial direction is rising, the Final baseline potential must be different than the Upper baseline potential. If the Initial direction is falling, the Final baseline potential must be different than the Lower baseline potential.
The waveform that is applied to the electrode in DPV is a sequence of pulses (see Figure 3). The total length of each pulse in the sequence is determined by the Period. The potential of the working electrode is stepped according to the Height for the period of time specified by the Width . The potential of the working electrode is then stepped back but only by the Height minus the Potential increment. The current is sampled at two points in each pulse. The first point is just prior to stepping the potential of the working electrode, and the second point comes at the end of each period just prior to stepping the potential of the working electrode back to begin the next pulse period. The waveform that is applied to the electrode in CDPV is identical to DPV on forward sweeps. On reverse sweeps in CDPV, the pulses are inverted.
Figure 3: DPV Waveform. Orange trace – Applied potential. Black squares – First current sample point. Note that the second current sample point is at the end of each pulse. A: Full waveform. B: Zoom of Waveform.
Advanced Tab
The Advanced Tab for this method allows you to change the behavior of the potentiostat during the induction period and relaxation period. By default, the potential applied to the working electrode during the induction and relaxation period will match the initial potential and final potential, respectively, as specified on the Basic Tab. You may override this default behavior, and you may also change the durations of the induction and relaxation periods if you wish.
Additionally, common to both DPV and CDPV, you can choose to invert the pulses during the experiment. Theoretically, the results will be the same since it is the differential current that is plotted. Please see the Theory section for more information.
Ranges Tab
Though AfterMath has the ability to automatically select the appropriate ranges for voltage and current during an experiment it is best to manually select the current range for any pulse technique. Please see the separate discussions on autoranging and the Ranges Tab for more information.
Post Experiment Conditions Tab
After the Relaxation Period, the Post Experiment Conditions are applied to the cell. Typically, the cell is disconnected but you may also specify the conditions applied to the cell. Please see the separate discussion on post experiment conditions for more information.
Typical Results
Below are the typical results for DPV for the oxidation of a solution of
in
phosphate buffer (see Figure 4, specific parameters are:
,
GC WE, period =
, width =
, height =
, potential increment =
).
Figure 4:Differential Pulse Voltammogram of a Potassium Ferrocyanide Solution in Phosphate Buffer
Below are the typical results for CDPV for the oxidation and reduction of in
phosphate buffer (see Figure 5, specific parameters were:
,
GC WE, period =
, width =
, height =
, potential increment =
). Crosshair tools have been added to show that peak positions and peak heights should be identical in CDPV for a fully reversible system.
Figure 5 : Cyclic Differential Pulse Voltammogram of a Potassium Ferrocyanide Solution in Phosphate Buffer
Theory
The following is a brief introduction to the theory of DPV. Please see Bard and Faulkner1 for a more complete description. Please see Drake et al.2 for a complete description of CDPV.
DPV is a technique that is designed to minimize background charging currents. The waveform in DPV is a sequence of pulses, where a baseline potential is held for a specified period of time prior to the application of a potential pulse. Current is sampled, at time , just prior to the application of the potential pulse. The potential is then stepped by a small amount (typically
) and current is sampled again, at time
at the end of the pulse. The potential of the working electrode is then stepped back by a lesser value than during the forward pulse such that baseline potential of each pulse is incremented throughout the sequence.
Consider a reaction , where
is reduced in a one electron step to
. At values sufficiently more positive than
no faradaic current flows before the potential step (to more negative values). The application of the potential step does not produce an appreciable increase in current. Thus, the differential is very small. At values significantly negative of
the baseline potential is reducing
at a maximum rate. The application of a small potential step (towards more negative values) is unlikely to increase the rate of reduction and hence the differential current is again small. Only at potentials around
will the differential current be significant. The period during the application of the baseline potential has
being reduced at some rate. The potential step (to more negative values) increases the rate of reduction and hence the differential current will be significant. Under normal conditions (pulse height
) the height of the peak can is given by the equation
where is the number of electrons,
is Faraday’s Constant (
),
is the electrode area (
),
is the diffusion coefficient (
),
is the concentration of electroactive species (
) and
is given by
where is the pulse height,
is the temperature (
) and
is the Universal Gas Constant (
).
As mentioned in the Advanced parameters tab, the direction of the pulse should not affect the results. Consider the reaction above , where
is reduced in a one electron step to
. At values sufficiently more positive than
no faradaic current flows before the potential step (towards more positive values). The change in current due to the potential step is also insignificant enough to cause faradaic current. Thus, the differential is very small. At values significantly negative of
the baseline potential is reducing
at a maximum rate. The application of a small potential pulse (towards more positive values) does not decrease the rate of reduction and hence the differential current is again small. Only at potentials around
will the differential current be significant. The period during the application of the baseline potential has
being reduced at some rate. The potential step (to more positive values) decreases the rate of reduction and hence the differential current will be significant. Hence, the direction of the potential step has no effect on the differential current observed.
Application
The first example uses DPV to examine the pH dependence of redox potential for a electron and proton transfers in trytophan and tyrosine. Sjödin et al.3 used the pH dependence of the redox potential to calculate values for different reaction pathways and thus determine that the mechanism can be a one step or two steps depending on several factors.
The second example uses DPV to examine the quantized double layer charging of hexanethiolate-coated monolayer-protected clusters (AuMPCs). Miles and Murray used DPV to resolve 13 individual peaks related to
core charging over a
window in
at lowered temperatures. Though peaks are visible using CV, DPV provides the necessary resolving power, by suppressing background currents, to separate out all 13 peaks. This is a wonderful example highlighting the power of DPV.
References
1. Faulkner, L. R.; Bard, A. J. Polarography and Pulse Voltammetry, Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New Jersey, 2000; 261-304.
2. Drake, K. F.; Van Duyne, R. P.; Bond, A. M. J. Electroanal. Chem. 1978, 89, 231-246.
4. Miles, D. T.; Murray, R. W. Anal. Chem. 2003, 75, 1251–1257.
Additional Links
Links: Electrochemist’s Guide, AfterMath User’s Guide, AfterMath Main Support Page
Related Techniques: Square Wave Voltammetry (SWV), Normal Pulse Voltammetry (NPV)
Controlled Current Bulk Electrolysis

This article is part of the AfterMath Data Organizer Electrochemistry Guide
Controlled current bulk electrolysis is analogous to chronopotentiometry, the major difference being the use of larger area electrodes in bulk electrolysis. Users are directed to the wiki regarding chronopotentiometry for a more detailed description regarding setup, theory and application.
Ramp Chronopotentiometry (RCP)

This article is part of the AfterMath Data Organizer Electrochemistry Guide
Detailed Description
Like most of the other electrochemical techniques offered by the AfterMath software, this experiment begins with an induction period. During the induction period, a set of initial conditions is applied to the electrochemical cell and the cell is allowed to equilibrate to these conditions. The default initial condition involves holding the working electrode current at the Initial Current for a brief period of time (i.e., 3 seconds).
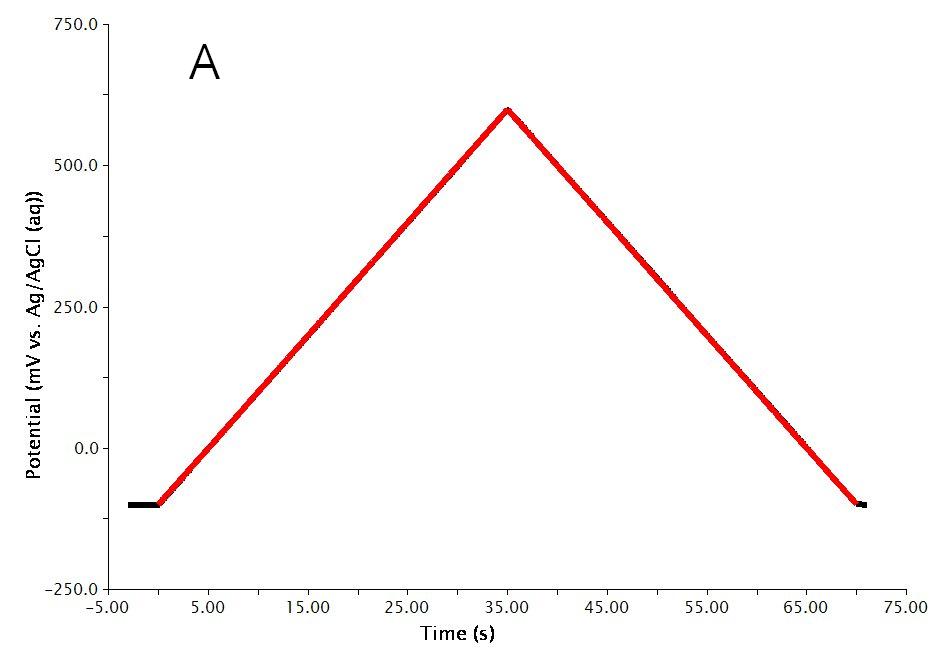
After the induction period, the current of the working electrode is swept linearly at the specified Sweep Rate to the Final Current.
After the sweep has finished, the experiment concludes with a relaxation period. The default condition during the relaxation period involves holding the working electrode current at the final current for an additional brief period of time (i.e., 1 seconds).
At the end of the relaxation period, the post experiment idle conditions are applied to the cell and the instrument returns to the idle state.
The working electrode potential is plotted as a function of the current applied to the working electrode, resulting in a potentiogram.
Parameters Setup
The parameters for this method are arranged on various tabs on the setup panel. The most commonly used parameters are on the Basic tab, and less commonly used parameters are on the Advanced tab. Additional tabs for Ranges tab and Post Experiment Idle Conditions tab are common to all of the electrochemical techniques supported by the AfterMath software.
Basic Tab
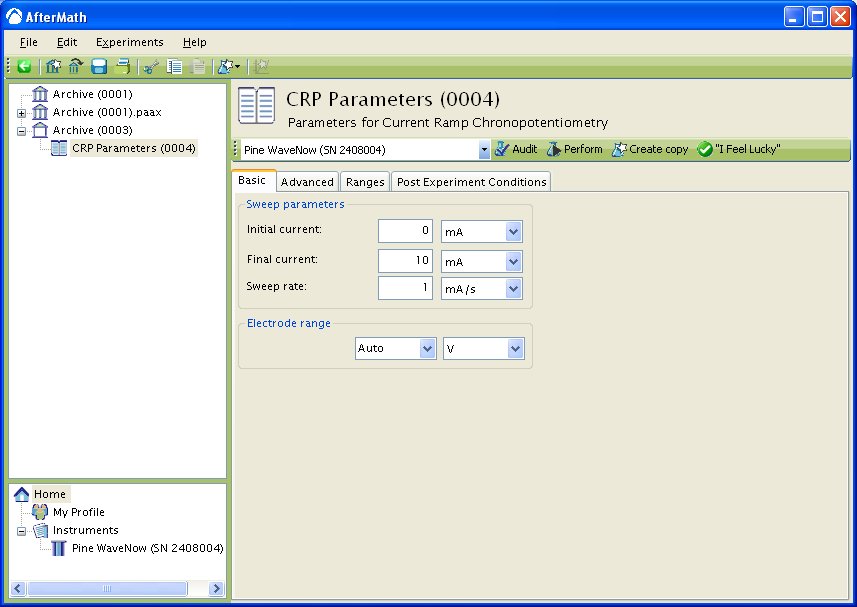
You can click on the “I Feel Lucky” button (located at the top of the setup) to fill in all the parameters with typical default values. You will no doubt need to change the Initial Current, Final Current, and Sweep Rate to values which are appropriate for the electrochemical system being studied.
Figure 1 : CRP Basic Parameters Setup
The Electrode Range on the Basic tab is used to specify the expected range of potentials. The potential of the electrode is dictated according to the Nernst equation, assuming a fully reversible system (see Theory section below), and will change to the value necessary to maintain the specified current. Therefore, if the choice of potential range is too small, actual potential may go off scale and the results will be truncated. If the potential range is too large, the potentiogram may have a noisy, choppy, or quantized appearance. Please see the ugly duckling webpage for an analogous situation in a voltammogram.
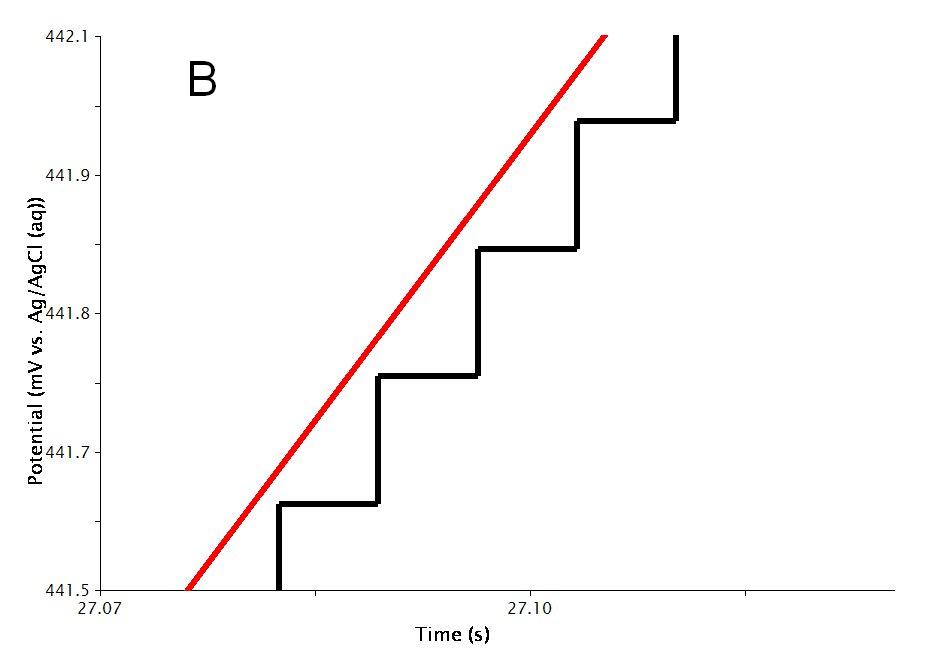
The actual waveform that is applied to the electrode is linear but not truly analog (see Figure 2A). The flat portions at the beginning and end of the waveform are the induction and relaxation periods, respectively. A typical sweep starts at an initial current and sweeps to the final current. The sweep is not perfect; in reality is consists of many small steps (see Figure 2B, orange trace, sweep rate = ) which are generated using the maximum available resolution of the potentiostat’s digital-to-analog converter (DAC).
Figure 2: CRP Waveform Details Showing A) the Total Waveform and B) a Magnified Waveform Showing the Applied Current (Orange) and Measured Current (Red).
Advanced Tab
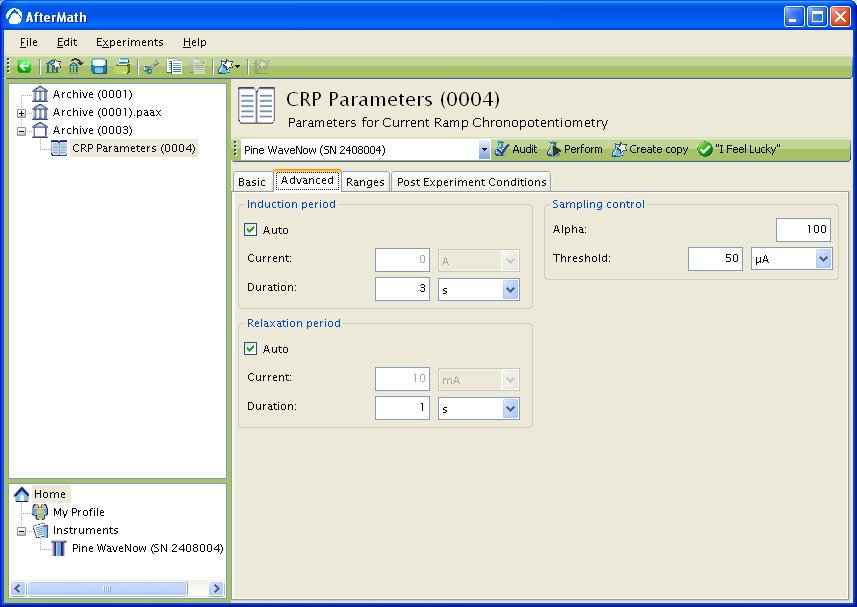
The Advanced Tab for this method (see Figure 3) allows you to change the behavior of the potentiostat during the induction period and relaxation period. By default, the current applied to the working electrode during the induction and relaxation period will match the initial current and final current, respectively, as specified on the Basic Tab. You may override this default behavior, and you may also change the durations of the induction and relaxation periods if you wish.
Other important parameters on the Advanced tab are found in the Sampling Control area. This area contains two parameters, Alpha and Threshold which control when and how samples are acquired during the sweep portion of the experiment.
Figure 3: Advanced parameters setup for Current Ramp Chronopotentiometry
As mentioned previously, the waveform applied to the electrode (see Figure 2) is not truly linear. The actual waveform is a staircase of small current steps. The duration of each small step is called the step period, and the step period is automatically chosen to take full advantage of the resolution of the potentiostat’s digital-to-analog converter.
The Alpha parameter controls the exact time within the step period at which the potential is sampled. A alpha value of zero means the potential is sampled at the start of the step period, immediately after a new current step is applied. An alpha value of 100 means the potential is sampled at the end of the step period, immediately before the next current step is applied. (See also the analogous discussion of the Alpha parameter in the description of cyclic voltammetry for more information.)
The Threshold parameter helps you to limit the amount of data retained as the potentiogram is acquired. The threshold parameter controls the interval between samples as the current is swept from one limit to another. As shown in the example in Figure 3, a data point is acquired every time the sweep moves 50 microamps. You could change the threshold from 50 microamps to a smaller interval (if you want to acquire more data) or to a greater interval (if you want to acquire less data).
It is very likely that you will need to change the Threshold parameter in order to obtain the best possible data from your particular electrochemical system. Extreme values for the threshold parameter can lead to undesirable results. A smaller threshold value, typically less than or equal to 5 microamps, produces smoother curves and larger data files. If you set the threshold parameter to zero, then the maximum number of data points is acquired (and the size of the resulting data file will be quite large). If you set the parameter to a very large interval, then the number of points acquired will be so small that the potentiogram appears sharp and jagged. (See also the analogous discussion of the Threshold parameter in the description of cyclic voltammetry for more information.)
Ranges Tab
AfterMath has the ability to automatically select the appropriate ranges for current and voltage during an experiment. However, you can also choose to enter the current and voltage ranges for an experiment. Please see the separate discussions on autoranging and the Ranges Tab for more information.
Post Experiment Conditions Tab
After the Relaxation Period, the Post Experiment Conditions are applied to the cell. Typically, the cell is disconnected but you may also specify the conditions applied to the cell. Please see the separate discussion on post experiment conditions for more information.
Typical Results
Typical results for a solution of ferrocene are shown in Figure 4. Potential can be plotted against time (see Figure 4A) or against current (see Figure 4B, specific parameters were: Ferrocene in
,
OD Pt WE,
sweep rate).
Figure 4 : A) Potential vs. Time and B) Potential vs. Current Chronopotentiograms for a Ferrocene Solution
Theory
The following is a very brief introduction to the theory of current ramp chronopotentiometry. Consult sources such as Bard and Faulker2 or Murray and Reilley3,4 for more detailed information.
CRP is a technique that, like CV, can be utilized to calculate a concentration or a diffusion coefficient. Consider a reaction with a formal potential
. As a current is applied to the working electrode,
begins getting reduced at the electrode surface, producing
. The potential of the electrode, E, moves to values characteristic of the
couple, based on a time-based Nernstian relation. As the concentration of
drops to zero at the electrode surface the potential starts to rapidly increase to more negative values. The resulting
curve is much like a potentiometric titration with a transition time (analogous to an equivalence point),
. The potential at one half
is
. The transition time is related to the concentration and diffusion coefficient of
through the expression
where is the concentration of
(
),
is the number of electrons,
is Faraday’s Constant (
),
is the electrode area (
),
is the diffusion coefficient (
) and
is the sweep rate (
).
For rapid electrode kinetics, the time-based Nernstian equation is
where is equal to
Finally, plotting should give a straight line with slope of
for a reversibile
curve.
References
1. He, P. Anal. Chem., 1995, 67, 986-992.
2. Faulkner, L. R.; Bard, A. J. Controlled-Current Techniques, Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New Jersey, 2000; 305-330.
3. Murray, R. W.; Reilley, C. N. J. Electroanal. Chem., 1962, 3, 64-77.
4. Murray, R. W.; Reilley, C. N. J. Electroanal. Chem., 1962, 3, 182-202.
Additional Resources
Cyclic Current Ramp Chronopotentiometry (CCP)

This article is part of the AfterMath Data Organizer Electrochemistry Guide
Detailed Description
Like most of the other electrochemical techniques offered by the AfterMath software, this experiment begins with an induction period. During the induction period, a set of initial conditions is applied to the electrochemical cell and the cell is allowed to equilibrate to these conditions. The default initial condition involves holding the working electrode current at the Initial Current for a brief period of time (i.e., 3 seconds).
After the induction period, the current of the working electrode is swept linearly at the specified Sweep Rate between an upper and lower current.
After the sweeps have finished, the experiment concludes with a relaxation period. The default condition during the relaxation period involves holding the working electrode current at the final current for an additional brief period of time (i.e., 1 seconds).
At the end of the relaxation period, the post experiment idle conditions are applied to the cell and the instrument returns to the idle state.
The working electrode potential is plotted as a function of the current applied to the working electrode, resulting in a cyclic potentiogram.
Basic Tab
You can click on the “I Feel Lucky” button, located at the top of the setup (see Figure 1), to fill in all the parameters with typical default values. You will no doubt need to change the parameters to values which are appropriate for the electrochemical system being studied.
Figure 1: CCP Basic Parameters Setup
The Electrode Range on the Basic tab is used to specify the expected range of potentials. The potential of the electrode is dictated according to the Nernst equation, assuming a fully reversible system (see Theory section in CRP), and will change to the value necessary to maintain the specified current. Therefore, if the choice of potential range is too small, actual potential may go off scale and the results will be truncated. If the potential range is too large, the potentiogram may have a noisy, choppy, or quantized appearance. Please see the ugly duckling wiki for an analogous situation in a voltammogram. .
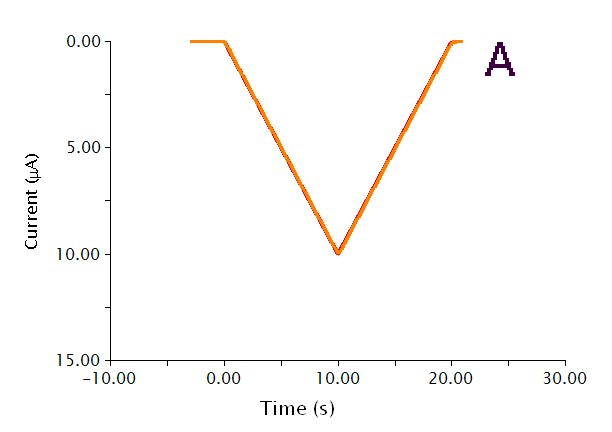
The actual waveform that is applied to the electrode is linear but not truly analog (see Figure 2A). The flat portions at the beginning and end of the waveform are the induction and relaxation periods, respectively. For a typical two sweep experiment, the sweep starts at an Initial current and sweeps to a Vertex current, then sweeps to the Final Current. The sweep is not perfect; in reality is consists of many small steps (see Figure 2B, orange trace) which are generated using the maximum available resolution of the potentiostat's digital-to-analog converter (DAC).
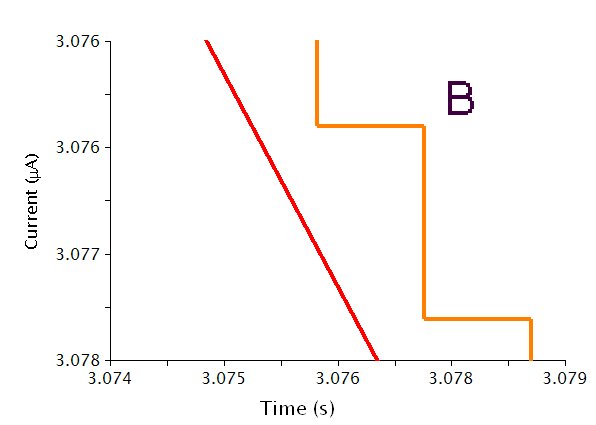
Figure 2: CCP Waveform Details Showing A) the Total Waveform and B) a Magnified Waveform that shows the Applied Current (Orange) and Measured Current (Red)
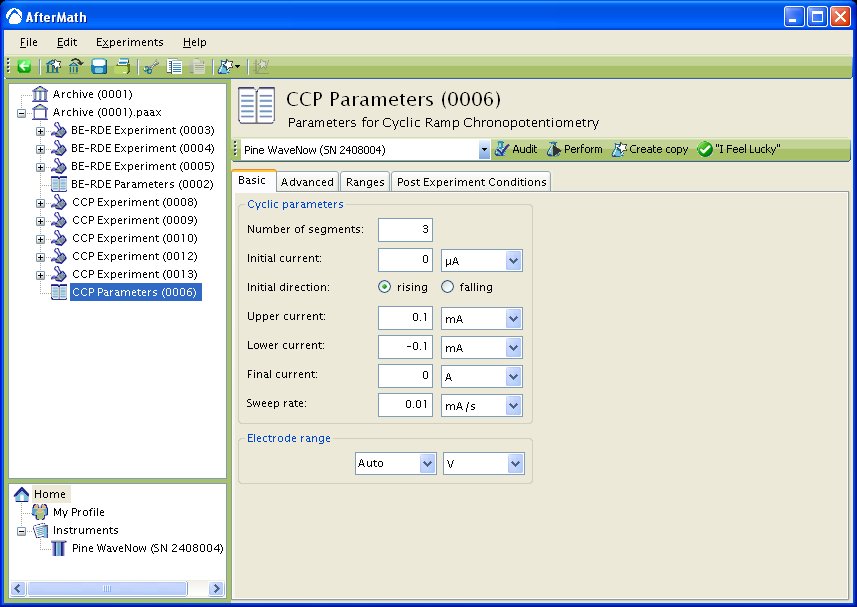
While cyclic current ramp potentiograms are typically two segments or one cycle, it is possible to choose any number of segments for an experiment. If you choose any odd number of segments greater than two, the parameters that must be entered are a little different than the two segment case (see Figure 3). You must choose an Initial Current, Upper Current, Lower Current, and Final Current. You must also choose whether the Initial direction is rising (sweep towards Upper Current) or falling (sweep towards Lower Current). If the Initial direction is rising, the Final Current must be different than the Lower Current. If the Initial direction is falling, the Final Current must be different than the Upper Current.
Figure 3: Basic setup for three segment CCP.
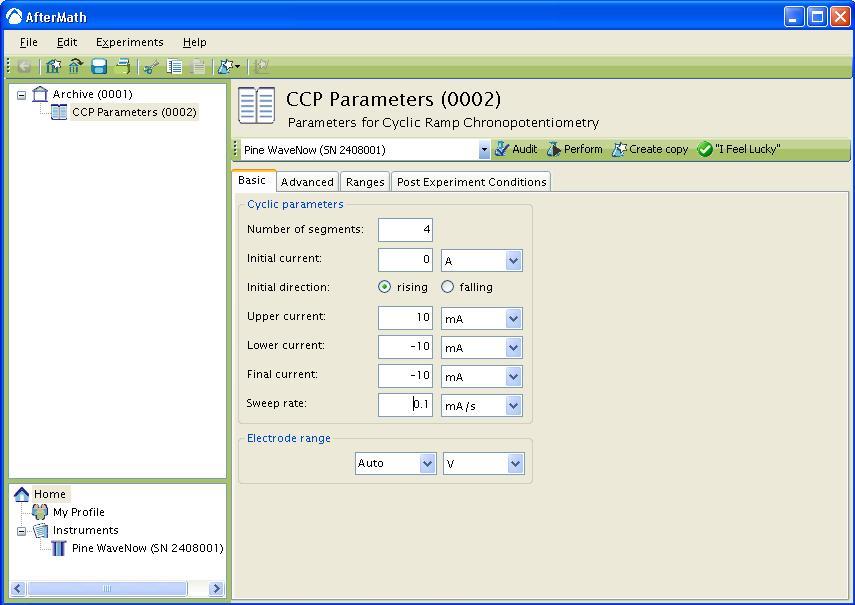
If you choose any even number of segments greater than two (see Figure 4), you must enter an Initial current, Upper current, Lower current, and Final current. You must also choose whether the first sweep is initially rising (sweep towards Upper current) or falling (sweep towards Lower current). If the Initial direction is rising, the Final current must be different than the Upper current. If the Initial direction is falling, the Final current must be different than the Lower current.
Figure 4: Basic setup for four segment CCP.
Avanced Tab
The Advanced Tab for this method (see Figure 5) allows you to change the behavior of the potentiostat during the induction period and relaxation period. By default, the current applied to the working electrode during the induction and relaxation period will match the initial current and final current, respectively, as specified on the Basic Tab. You may override this default behavior, and you may also change the durations of the induction and relaxation periods if you wish.
Other important parameters on the Advanced tab are found in the Sampling Control area. This area contains two parameters, Alpha and Threshold which control when and how samples are acquired during the sweep portion of the experiment.
Figure 5: Advanced parameters setup for Cyclic Current Ramp Chronopotentiometry
As mentioned previously, the waveform applied to the electrode (see Figure 2) is not truly linear. The actual waveform is a staircase of small current steps. The duration of each small step is called the step period, and the step period is automatically chosen to take full advantage of the resolution of the potentiostat's digital-to-analog converter.
The Alpha parameter controls the exact time within the step period at which the potential is sampled. A alpha value of zero means the potential is sampled at the start of the step period, immediately after a new current step is applied. An alpha value of 100 means the potential is sampled at the end of the step period, immediately before the next current step is applied. Please see the Advanced Parameter Tab section of CV for an analogous situation in a voltammogram.
The Threshold parameter helps you to limit the amount of data retained as the potentiogram is acquired. The threshold parameter controls the interval between samples as the current is swept from one limit to another. As shown in the example in Figure 3, a data point is acquired every time the sweep moves . You could change the threshold from
to a smaller interval (if you want to acquire more data) or to a greater interval (if you want to acquire less data).
It is likely that you will have to change the default value based on your experimental setup in order to obtain the best possible data. Extreme values for the threshold parameter can lead to undesirable results. A smaller threshold value, typically less than or equal to , produces smoother curves and larger data files. If you set the threshold parameter to zero, then the maximum number of data points is acquired (and the size of the resulting data file will be quite large). If you set the parameter to a very large interval, then the number of points acquired will be so small that the potentiogram appears sharp and jagged. Please see the CV article for an analogous situation in a voltammogram.
Ranges Tab
AfterMath has the ability to automatically select the appropriate ranges for voltage and current during an experiment. However, you can also choose to enter the voltage and current ranges for an experiment. Please see the separate discussions on autoranging and the Ranges Tab for more information.
Post Experiment Conditions Tab
After the Relaxation Period, the Post Experiment Conditions are applied to the cell. Typically, the cell is disconnected but the user may also specify the conditions applied to the cell. Please see the separate discussion on post experiment conditions for more information.
Typical Results
The chronopotentiogram for a solution of ferrocene look similar to the results for a series of successive titrations except that the current is not ramped through the transition points. Potential can be plotted against time (see Figure 6A) or against current (see Figure 6B, specific parameters were: Ferrocene in
,
OD Pt WE,
sweep rate ).
Figure 6: Chronopotentiograms Depicting A) Potential vs. Time and B) Potential vs. Current for a Ferrocene Solution.
Theory
Please see the wiki related to CRP, Bard and Faulker2 or Murray and Reilley's3,4 original papers for a more detailed discussion on the theory of CCP.
References
Additional Resources
Links: Electrochemist's Guide, AfterMath User's Guide, AfterMath Main Support Page
Related Techniques: chronopotentiometry, current ramp chronopotentiometry
Read More
Cell and Circuit Switching

This article is part of the AfterMath Data Organizer Electrochemistry Guide
Circuit Switching
Most electrochemical instruments are designed to perform a wide range of electrochemical techniques. Different techniques make use of different portions of the circuitry within the instrument, and this means that circuit switching is likely to occur when configuring the instrument for a particular method.
For example, the feedback loop circuitry for a galvanostatic method actively monitors the working electrode current, but for a potentiostatic method, the feedback circuitry must monitor the working electrode potential. Different feedback paths are switched in and out of the circuit depending upon whether the working electrode is operating in potentiostatic or galvanostatic mode. Still other methods require passive measurement of the open circuit potential, meaning that the active feedback loop must be switched out of the circuit entirely. Circuit switching also occurs when changing the current measurement sensitivity (i.e., the current range) or the amount of stability filtering in the feedback loop (i.e., the response time).
The term cell switching refers to making (or breaking) the connection between the instrument and the external electrochemical cell. In some cases, this switching occurs manually (as you physically connect/disconnect cell cables), but in many cases this switching occurs under software control (via internal instrument relays).
Each time a cell or circuit switching action occurs, the instrument is likely to lose control of the external electrochemical cell for a brief period (typically on the order of a few milliseconds). As the instrument regains control of cell, various current transients may occur at the working electrode. These transients are often harmless and decay away rather rapidly. If your electrochemical system is particularly sensitive, however, these transients may interfere significantly with your experiments.
For systems where such transients are harmless, a one to three second long induction period at the beginning of an experiment assures that the random transients will not affect the data recorded during an experiment. In other cases, special steps (see below) must be taken to prevent such transients.
Minimizing Switching and Transients
The best way to minimize unwanted and potentially harmful current transients is to carefully make sure that the signal applied to the working electrode at the beginning and end of the experiment is exactly the same as the signal applied to the working electrode during the idle periods in between experiments.
When no experiment is being performed, the instrument is said to be in its idle mode. Although the instrument is idle, it can still maintain a steady potential (or current) at the working electrode. The precise signal levels can be adjusted from the Instrument Status window. In general, the idle signal level should be set at a potential (or current) at which your electrochemical system is stable.
When specifying a new experiment to be performed, carefully adjust the initial conditions and the induction period conditions so that they exactly match the idle conditions which prevail before the experiment begins. This means that the initial signal level should match the idle signal level. On those instruments which permit adjustment of the idle current range and idle filtering settings, you should further strive to match the idle filter and range settings so that they match those which will be used during the experiment.
Finally, each electrochemical technique allows you to specify the idle conditions that will prevail after the experiment is completed. These post-experiment idle conditions should also be selected so that they exactly match the final conditions which prevail during the relaxation period at the end of the experiment.
Additional Resources
Chronoamperometry (CA)

This article is part of the AfterMath Data Organizer Electrochemistry Guide.
Detailed Description
Like most of the other electrochemical techniques offered by the AfterMath software, this experiment begins with an induction period. During the induction period, a set of initial conditions is applied to the electrochemical cell and the cell is allowed to equilibrate to these conditions. The default initial condition involves holding the working electrode potential at the initial potential for a brief period of time (i.e., 3 seconds). After the induction period, the potential of the working electrode is stepped to a specified potential for a period of time. After the step has finished, the experiment concludes with a relaxation period. The default condition during the relaxation period involves holding the working electrode potential at the initial potential for an additional brief period of time (i.e., 1 seconds). At the end of the relaxation period, the post experiment idle conditions are applied to the cell and the instrument returns to the idle state.
Current is plotted as a function of time, resulting in a chronoamperogram. You may also choose to do some post experiment processing in order to generate a Cottrell plot.
Parameter Setup
The parameters for this method are arranged on various tabs on the setup panel. The most commonly used parameters are on the Basic tab. Additional tabs for Ranges and post experiment idle conditions are common to all of the electrochemical techniques supported by the AfterMath software. Finally, a Post Experiment Processing tab deals with manipulating the data automatically when the experiment is finished.
Basic Tab
You can click on the “I Feel Lucky” button (located at the top of the setup) to fill in all the parameters with typical default values (see Figure 1). You will no doubt need to change the Potential and Hold time in the Forward step period box to values which are appropriate for the electrochemical system being studied. You may also want to change the Number of intervals in the Sampling Control box.
Figure 1: Basic Chronoamperometry Setup
The Electrode Range on the Basic tab is used to specify the expected range of current. If the choice of electrode range is too small, actual current may go off scale and be truncated. If the electrode range is too large, the chronoamperogram may have a noisy, choppy, or quantized appearance.
Some Pine potentiostats (such as the WaveNow and WaveNano portable USB potentiostats) have current autoranging capability. To take advantage of this feature, set the electrode range parameter to “Auto”. This allows the potentiostat to choose the current range “on-the-fly” while the chonoamperogram is being acquired.
The waveform that is applied to the electrode is a simple pulse to the Potential listed in the Forward step period box. Note that the actual waveform that is measured (see Figure 2, red trace) fluctuates slightly compared to the applied potential (see Figure 2, black trace).
Figure 2: Waveform for CA. Black trace = applied potential, Red trace = measured potential.
Ranges Tab
AfterMath has the ability to automatically select the appropriate ranges for voltage and current during an experiment. However, you can also choose to enter the voltage and current ranges for an experiment. Please see the separate discussions on autoranging and the Ranges Tab for more information.
Post Experiment Conditions Tab
After the Relaxation Period, the Post Experiment Conditions are applied to the cell. Typically, the cell is disconnected but you may also specify the conditions applied to the cell. Please see the separate discussion on post experiment conditions for more information.
Post Experiment Processing Tab
Typical Results
The results for a solution of ferrocene in
are shown in Figure 4.
Figure 4: Chronoamperogram of a ferrocene solution using a potential = and a
Pt WE.
If you selected to automatically generate Cottrell plots, the plots are under the other plots folder in the Archive navigation panel. Choosing Cottrell current displays a plot of (see Figure 5A). Choosing Cottrell charge displays a plot of
(see Figure 5B). Note that for the Cottrell Current plot, the level portion in the plot is actually the time prior to the current spike shown in Figure 4. That is, earlier time points are to the right in a Cottrell Current Plot. This is not the case for a Cottrell Charge plot because integrating the current with respect to time gives charge. The endpoint in a Cottrell Charge plot is the total amount of charge passed during the experiment. Monitoring the charge passed during an experiment is a variant of chronoamperometry called Chronocoulometry. See the Applications section for an example of Chronocoulometry.
Figure 5 : Post experiment processing plots. A – Cottrell Current , B – Cottrell Charge
. Conditions as listed in Figure 4.
The Cottrell current plot is a useful diagnostic tool to examine that your species of interest is freely diffusion in solution. Upon applying the potential step, the current initially spikes, then begins trail off. As will be explained in more detail in the Theory section, the current during the trailing off period is a diffusion-limited current dictated by the Cottrell equation. Examining the Cottrell Current plot in this region reveals that the current is linear with respect to (see black ellipse in Figure 6).
Figure 6: Highlight of Diffusion-limited Current in Cottrell Current Plot.
The addition of a Baseline tool to the diffusion limited current region allows for calculation of the diffusion coefficient for the species of interest if the concentration and electrode area are known (see Figure 7). First you will have to delete the region of the Cottrell Plot where current is not diffusion limited. Use the Point Selection Tool to delete the unwanted points of the Cottrell Plot. Next, add a baseline tool by right clicking on the leftover point and select Add Tool » Baseline. Manipulate the control points to provide an adequate fit. AfterMath automatically provides the slope and intercept for the Baseline tool.
Figure 7: Addition of Baseline Tool in Diffusion-limited Current Region.
The slope of the line in the plot is given by the equation
where is the number of electrons,
is Faraday’s Constant
,
is the electrode area
,
is the diffusion coefficient
, and
is the concentration
. In the example above,
is calculated to be
.
Theory
The theory section is split into two segments. The first segment deals with Chronoamperometry (CA) and the second section deals with Chronocoulometry (CC). Chronoamperometry leads to Chronocoulometry natually since charge is obtained by integrating current with respect to time.
Chronoamperometry
The following is a basic description of the theory behind Chronoamperometry. Please see the literature1 for a more detailed description of the technique. Consider a reaction with a formal potential
. In general, the potential step applied to the working electrode should be sufficiently more negative than
such that reduction of
to
is complete at the surface of the electrode (i.e. surface concentration of
at the electrode surface is
). When this occurs, the current is diffusion-limited, much like the current that flows in CV after the potential of the electrode sweeps past
.
When the current is diffusion-limited in CA, the current-time response is described by the Cottrell2 equation
where
is the number of electrons,
is Faraday’s Constant
,
is the electrode area
,
is the diffusion coefficient
, and
is the concentration
. As described in the Typical Results section, plotting
gives a slope that contains the diffusion coefficient,
.
Chronocoulometry
The following is a brief description of chronocoulometry. Please see the literature1 for a more detailed description of the technique. Chronocoulometry is advantages in some ways over chronoamperometry. First is that the signal grows with time, meaning that the later portion of the experiment are least distorted by the nonideal potential rise, giving better signal-to-noise ratios. Second, integrating smooths random noise making the data cleaner. Third, contributions from double-layer charging and reactions of adsorbed species can be separating from those of freely diffusion species. The cumulative charge passed during the experiment is given by the equation
where the parameters are as described in the above section. Typically, a plot of has a non-zero y-intercept. This intercept is related to double-layer charging and reduction of adsorbed
. The overall equation describing the charge is then given by
where is the charge due to double-layer charging and
is the charge due to reduction of adsorbed
.
and
are not easily separated and usually require additional experiments such as double potential step chronoamperometry. However, approximations for
can be made by performing the same potential step in a solution of only electrolyte. This is only an approximation because the true double-layer charging will be influenced by adsorbed
.
The Application section in the next tab contains examples of both Chronoamperometry and Chronocoulometry.
Application
In the first example, Tennyson et al.3 used chronoampometry to determine the diffusion coefficients (D) and number of electrons (n) for a series of indirectly connected bimetallic complexes. In this instance, the researchers used microelectrodes to generate steady-state currents. Plotting of the function
allows for the calculation of without knowledge of
or
. Though the experiments are relatively simple and straightforward, the researchers then used these values for more complicated electrochemical experiments that enabled them to determine the degree of electronic coupling between the two metallic centers. Understanding the degree of electronic coupling could allow for facilitation to otherwise inaccessible catalysts and materials.
The next example uses chronoamperometry to measure extremely small diffusion coefficients of redox polyether hybrid cobalt bipyridine molten salts. Crooker and Murray4 performed chronoamperometry on a series of undiluted molten salts and were able to obtain diffusion coefficients as low as . The researchers went on to obtain heterogeneous rate constants
using CV and were able to show that the reaction remains quasireversible despite small
rates because
values are so low.
The next example uses chronoamperometry to directly measure rate constants. Smalley et al.5 examined a series of monolayers terminated with either a ferrocene or ruthenium redox moiety. For monolayers containing more than 11 methylene units, chronoamperometry was used to determine the heterogeneous rate constants . The researchers also determined preexponential factors and found them to be much lower that expected based aqueous solvent dynamics.
The fourth example uses chronocoulometry. Wolfe et al.6 prepared a series of ferrocenated hexanethiolate protected Au nanoparticles. Normallly, TGA would be used to calculate the number of thiolates per nanoparticle. However, in this case, TGA was inconclusive due to a slow loss of mass over the applied temperature range. The researchers instead monitored the charge pass over time for solution of nanoparticles with known concentrations. Knowing the total charge passed and the particle concentration allowed them to determine the number of ligands per nanoparticle. This is a good example of how electrochemistry can be used in place of a more traditional characterization technique.
The final example also uses chronocoulometry, but rather than using it for quantification purposes, the researchers use it to evoke a change in the system. Zhang et al.7 use chronocoulometry with predefined endpoints to produce Ag nanoparticles, confined on a electrode surface, with varying shapes and sizes. By varying the amount of charge passed the researchers were able to show that triangular nanoparticles oxidize first on the bottom edge, followed by triangular tips, followed by out-of-plane height. Since the researchers also coupled spectroscopy to their electrochemical experiments they were also able to show how the SPR band changes with shape evolution. This is a nice example of how electrochemistry can be used to evoke a change in a system rather than simply to monitor changes or determine physical parameters of the system.
References
- Faulkner, L. R.; Bard, A. J. Basic Potential Step Methods, Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New Jersey, 2000; 156-225.
- Cottrell, F. G. Z. Physik, Chem., 42, 1902, 385.
- Tennyson, A. G.; Khramov, D. M.; Varnado, C. D. Jr.; Creswell, P. T.; Kamplain, J. W.; Lynch V. M.; Bielawski, C. W.; Organometallics, 2009, 28, pp 5142–5147.
- Crooker, J. C.; Murray, R. W. Anal. Chem., 2000, 72, pp 3245–3252.
- Smalley, J. F.; Finklea, H. O.; Chidsey, C. E. D.; Linford, M. R.; Creager, S. E.; Ferraris, J. P.; Chalfant, K.; Zawodzinsk, T.; Feldberg, S. W.; Newton, M. D. J. Am. Chem. Soc., 2003, 125, pp 2004–2013.
- Wolfe, R. L.; Balasubramanian, R.; Tracy, J. B.; Murray, R. W. Langmuir, 2007, 23 (4), pp 2247–2254.
- Zhang, X.; Hicks, E. M.; Zhao, J.; Schatz, G. C.; Van Duyne, R. P. Nano Lett., 2005, 5, pp 1503–1507